Animal movement and interaction with their environment

Model : AntsWorld
Simile version : 4.0
Date added : 2004-10-20
Keywords : Hexagonal grid ; Association submodel ; Movement ; One sided enumeration ; Spatial modelling ;

Description

In this model, a population of animals (called ants) is created and the individuals move around at random. The area in which they move is represented by a grid of hexagons.

An association model is created to relate each individual to the hexagon it currently occupies. The technique of one-sided enumeration is used to make this association; it is vital that it happens efficiently, because it changes each time step. In this case the position of each ant is used to determine the index of the submodel instance for the hexagon containing it.

Having this association allows the ant to interact with their immediate environment. In this model, the interaction is simple, and one-way; the ants deposit a 'pheromone' which collects in each hexagonal patch. Since all the ants are in the middle of their area when they appear, and subsequently wander off at random, the pheromone concentration is greatest in the centre (see diagrams).

This prototypical model could easily be enhanced to include more aspects of real ant behaviour. The association betweeen ants and their environment could be made to include neighbouring hexagons as well as those actually occupied, and ants could be made to respond to levels of pheromone in the cells surrounding their own, as well as the presence of other ants.

Files

Model file Click on the icon to download the model file. (You will need Simile to examine and run the model. A free evaluation version is available from the products page.) Some browsers may attempt to display the model file, rather than open it in Simile; in this case, use the browser back button to return to this page, and use the context menu (invoked by right-clicking on the link) to save the target file to disk.
antsworld.sml	The 'ants world' model
antsworld.shf	Helper state file including locations of ants and distribution of pheromone

Diagram

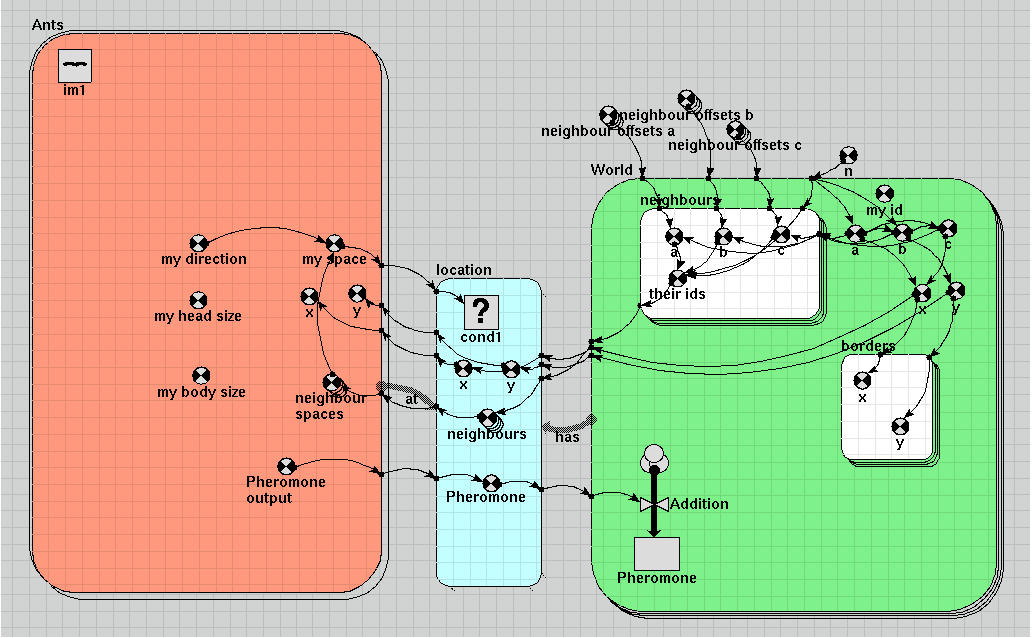
Equations

Equations in antsworld
 
Variable   n
	n = int(sqrt(size(World))) 
 
Variable   neighbour offsets a
	neighbour offsets a = [0,1,1,0,-1,-1] 
 
Variable   neighbour offsets b
	neighbour offsets b = [1,0,-1,-1,0,1] 
 
Variable   neighbour offsets c
	neighbour offsets c = [-1,-1,0,1,1,0] 

Equations in Ants
 
Immigration   im1
	im1 =  0.1 
 
Variable   Pheromone output
	Pheromone output = 1 
 
Variable   my body size
	my body size = 2 
 
Variable   my direction
	my direction = ceil(rand_var(0,6)) 
 
Variable   my head size
	my head size = 1 
 
Variable   my space
	my space = infront=element(last([neighbour_spaces]),my_direction),if time()==init_time() then 5102 elseif infront>0 then infront else prev(1) 
	Where:
		my_direction=my direction
		[neighbour_spaces]=neighbour spaces 
 
Variable   neighbour spaces
	neighbour spaces = [neighbours_at] 
	Where:
		[neighbours_at]= ../location/neighbours (to Ants in at) 
 
Variable   x
	x = x_at 
	Where:
		x_at= ../location/x (to Ants in at) 
 
Variable   y
	y = y_at 
	Where:
		y_at= ../location/y (to Ants in at) 

Equations in location
 
Condition   cond1
	cond1 = index(1) is my_space_at 
	Where:
		my_space_at= ../Ants/my space (from Ants in at) 
 
Variable   Pheromone
	Pheromone = Pheromone_output_at 
	Where:
		Pheromone_output_at= ../Ants/Pheromone output (from Ants in at) 
 
Variable   neighbours
	neighbours = [their_ids_has] 
	Where:

		[their_ids_has]= ../World/neighbours/their ids (from World in has) 
 
Variable   x
	x = x_has 
	Where:
		x_has= ../World/x (from World in has) 
 
Variable   y
	y = y_has 
	Where:
		y_has= ../World/y (from World in has) 

Equations in World
 
Compartment   Pheromone
	Initial value = 0
	Rate of change =  + Addition
 
Flow   Addition
	Addition = sum({Pheromone_has}) 
	Where:
		{Pheromone_has}= ../location/Pheromone (to World in has) 
 
Variable   a
	a = ceil(index(1)/n)-ceil(n/2) 
	Where:
		n= ../n 
 
Variable   b
	b = index(1)-n*a-ceil(n*n/2) 
	Where:
		n= ../n 
 
Variable   c
	c = -a-b 
 
Variable   my id
	my id = index(1) 
 
Variable   x
	x = 50+(a-c)* 0.866 
 
Variable   y
	y = 50+b* 1.5 

Equations in borders
 
Variable   x
	x = off=sqrt(3/4),x+element([0,off,off,0,-off,-off],index(1)) 
	Where:
		x= ../x 
 
Variable   y
	y = y+element([1, 0.5, -0.5,-1, -0.5, 0.5],index(1)) 
	Where:
		y= ../y 

Equations in neighbours
 
Variable   a
	a = a+element([neighbour_offsets_a],index(1)) 
	Where:
		a= ../a
		[neighbour_offsets_a]= ../../neighbour offsets a 
 
Variable   b
	b = b+element([neighbour_offsets_b],index(1)) 
	Where:
		b= ../b
		[neighbour_offsets_b]= ../../neighbour offsets b 
 
Variable   c
	c = c+element([neighbour_offsets_c],index(1)) 
	Where:
		c= ../c
		[neighbour_offsets_c]= ../../neighbour offsets c 
 
Variable   their ids
	their ids = if all([a,b,c]> - (n/2)) and all([a,b,c]
Results
|
This image shows the distribution of pheromone over the grid are after 3000 time units: 



|	  
      
Copyright 2003-2024 Simulistics Ltd