Worked example: water flow
between soil layers

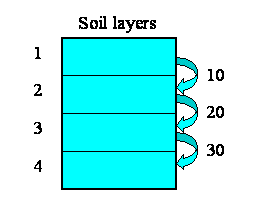
We want to model the movement of water between four soil layers. Each
layer has a compartment representing the amount of water held in that
layer. Water draining out of one layer will enter the layer immediately
below it. The following diagram illustrates the system, with notional
rates of 10, 20 and 30 units of water per unit of time flowing between the
layers.

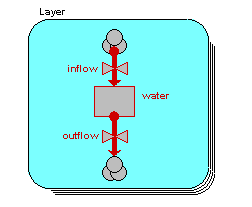
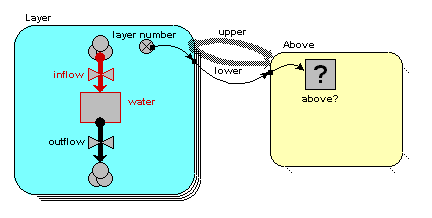
We begin by constructing a fixed-membership submodel to represent the
four layers: each instance represents one layer. Each layer has a single
compartment, for the amount of water in that layer. The compartment has a
flow in, for the water flowing into it from the layer above, and a flow
out, for the water flowing from that layer to the layer below. (There may
well be other flows, but they are not relevant to the use of association
submodels.) At this stage, we have not entered any values, so all the
model elements are red.

Now, some of the elements have an association with each other - the
relationship of one being immediately above the other.

• Layer 1 is above layer 2
• Layer 2 is above layer 3
• Layer 3 is above layer 4

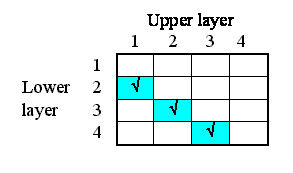
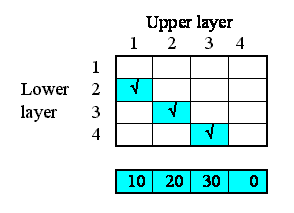
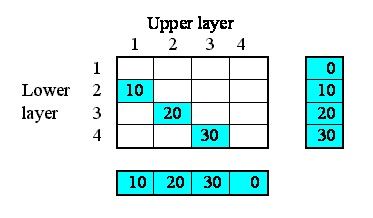
But potentially there could be associations between each instance and
all the other instances. In other words, the relationships that we have,
in this particular system, are a subset of all the 4x4 relationships that
potentially could exist. We can represent this in a matrix (below), with
as many rows and columns as we have instances in our submodel.

The ticks show when the relationship of being next to exists between an
upper layer and a lower layer. Note that, in this particular problem, the
relationship is not symmetrical: layer 1 is above layer 2, and not the
other way around. In some cases, the relationship could be symmetrical
(like neighbourliness in a spatial grid), but not here.

We will now modify the model diagram to represent the fact that this
relationship exists between layers.

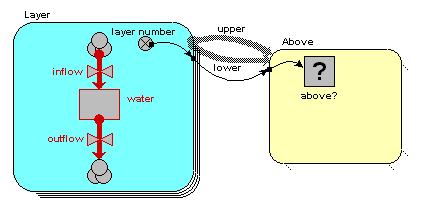
Quite a lot has happened here, so I'll explain the changes
one-by-one.

We are now in a position to pass information between pairs of instances
of the "Layer" submodel. In this case, we want to pass the value for the
amount of water passing out of one layer to the layer below it.

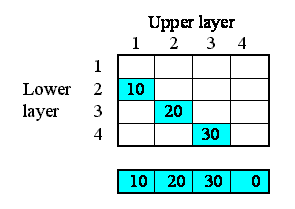
We begin by specifying how much water flows out of each layer to the
layer below. Here, I've assumed 10 units per unit of time from the first
layer, 20 from the second, and so on. In this particular context, this
value is a property of each layer: each layer calculates the flow out of
it. This could be because the flow is related to the water content of that
layer, for example. We show this as a set of value beneath each column,
since the columns refer to the upper layer.

In terms of our model diagram, the fact that we have provided values for
the four outflows simply means that the outflow arrow is now black:

Now, each of the first three of these outflows in fact constitutes an
interflow between the two layers: i.e. it is a property of the relationship
between the two layers. In our matrix, we can therefore enter the values
in the boxes corresponding to the linkage between the upper and lower
layers:

On the model diagram, we add a variable inside the "Above" submodel,
here called "interflow", and take an influence arrow to it from "outflow".
This shows that (in this particular model) the interflow is calculated from
the each soil layer's outflow.

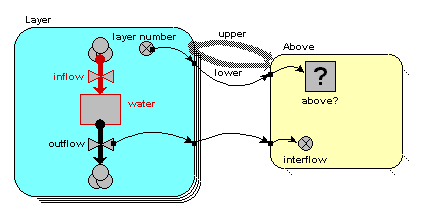
Because we are inside the "Above" association submodel, we could
(potentially) set interflow to the outflow from the upper layer or the
outflow from the lower layer. The first has the local name "outflow" in the equation dialogue box, while the second
has the local name "outflow_0". In this particular model, we want it to be
from the upper layer, so we select the variable

However, we know that the interflow between layers becomes the inflow
for the lower layer. In our matrix, we show this fact by copying the
interflow values across to the right, to the column representing the inflow
into each layer.

In the model diagram, we draw an influence arrow from the "interflow"
variable in the "Above" submodel to the "inflow" variable in the "Layer"
submodel.

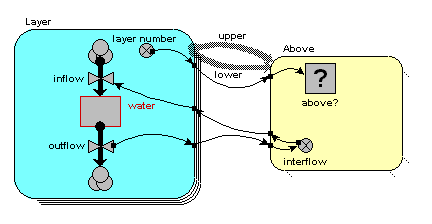
When we look inside the equation dialogue window for inflow, we get a
bit of a surprise. We expect to see interflow as an influencing variable,
but:

• we actually see it offered twice, with local names "interflow" and
  "interflow_0"; and
• each of these is a list (i.e. {interflow} and {interflow_0}), rather
  than a normal variable.

It's offered twice, because we could (potentially) be interested in the
interflow values relating to the upper layer (those under the columns in
the matrix above); or the interflows relating to the lower layer (the
interflows to the right of the rows in the matrix above). We want the
latter, so we choose {interflow_0}.

Why is the information from the submodel a list rather than a scalar
variable? Well, potentially there could be as many values as there are
soil layers. In this particular case, we happen to have put in a condition
that restricts it to one value for three of the layers, and none at all for
one layer, so our list will contain only zero or one value, depending on
the layer. But if we had allowed water to flow directly from a layer to
any layer below it, then the list could contain several values.

Anyway, the fact that it's in a list means that we have to extract a
single value by summing up the elements of this list. So the actual
equation we use for inflow is:

inflow = sum{interflow_0})

In: Contents >> Working with submodels >> Association submodels