Main menu
You are here
Animal movement and interaction with their environment
In this model, a population of animals (called ants) is created and the individuals move around at random. The area in which they move is represented by a grid of hexagons.
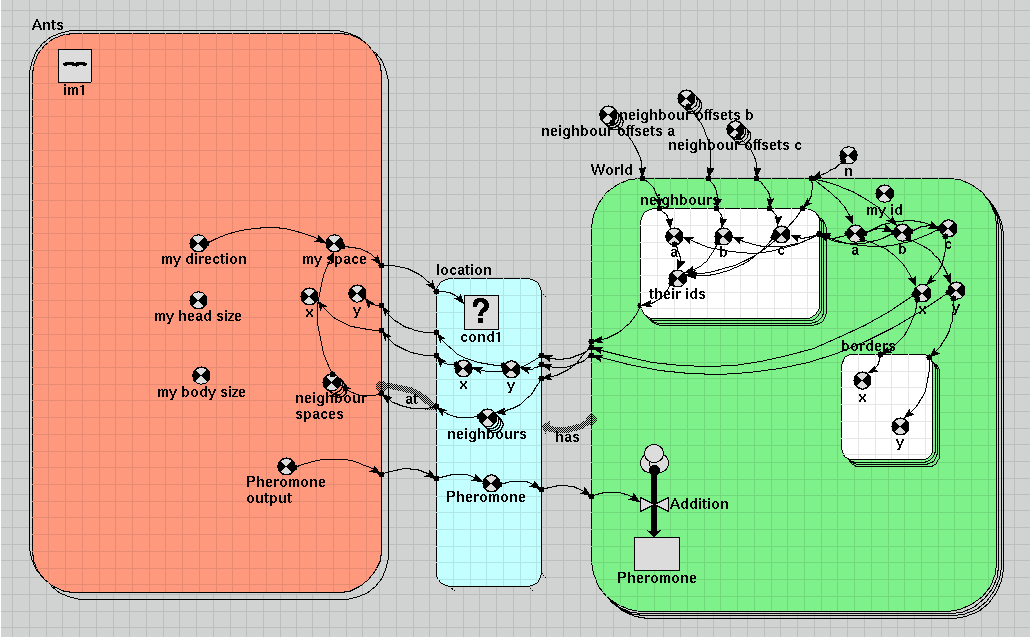
An association model is created to relate each individual to the hexagon it currently occupies. The technique of one-sided enumeration is used to make this association; it is vital that it happens efficiently, because it changes each time step. In this case the position of each ant is used to determine the index of the submodel instance for the hexagon containing it.
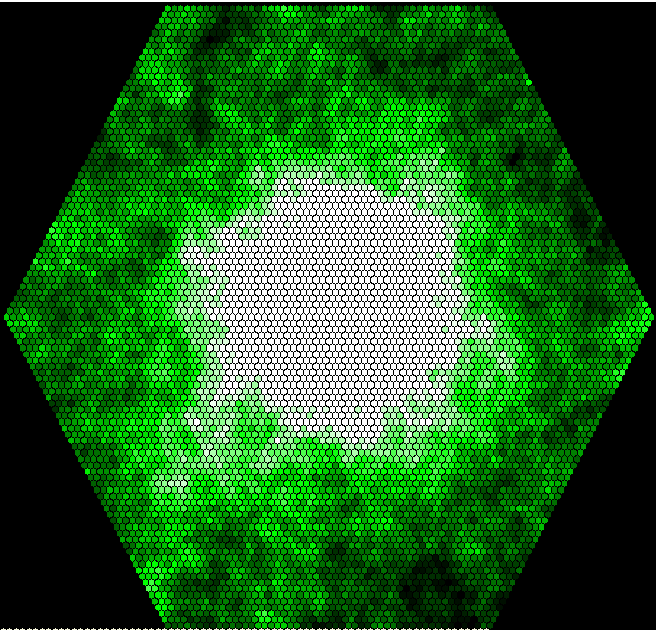
Having this association allows the ant to interact with their immediate environment. In this model, the interaction is simple, and one-way; the ants deposit a 'pheromone' which collects in each hexagonal patch. Since all the ants are in the middle of their area when they appear, and subsequently wander off at random, the pheromone concentration is greatest in the centre (see diagrams).
This prototypical model could easily be enhanced to include more aspects of real ant behaviour. The association betweeen ants and their environment could be made to include neighbouring hexagons as well as those actually occupied, and ants could be made to respond to levels of pheromone in the cells surrounding their own, as well as the presence of other ants.
Equations in antsworld
Variable n
n = int(sqrt(size(World)))
Variable neighbour offsets a
neighbour offsets a = [0,1,1,0,-1,-1]
Variable neighbour offsets b
neighbour offsets b = [1,0,-1,-1,0,1]
Variable neighbour offsets c
neighbour offsets c = [-1,-1,0,1,1,0]
Equations in Ants
Immigration im1
im1 = 0.1
Variable Pheromone output
Pheromone output = 1
Variable my body size
my body size = 2
Variable my direction
my direction = ceil(rand_var(0,6))
Variable my head size
my head size = 1
Variable my space
my space = infront=element(last([neighbour_spaces]),my_direction),if time()==init_time() then 5102 elseif infront>0 then infront else prev(1)
Where:
my_direction=my direction
[neighbour_spaces]=neighbour spaces
Variable neighbour spaces
neighbour spaces = [neighbours_at]
Where:
[neighbours_at]= ../location/neighbours (to Ants in at)
Variable x
x = x_at
Where:
x_at= ../location/x (to Ants in at)
Variable y
y = y_at
Where:
y_at= ../location/y (to Ants in at)
Equations in location
Condition cond1
cond1 = index(1) is my_space_at
Where:
my_space_at= ../Ants/my space (from Ants in at)
Variable Pheromone
Pheromone = Pheromone_output_at
Where:
Pheromone_output_at= ../Ants/Pheromone output (from Ants in at)
Variable neighbours
neighbours = [their_ids_has]
Where:
[their_ids_has]= ../World/neighbours/their ids (from World in has)
Variable x
x = x_has
Where:
x_has= ../World/x (from World in has)
Variable y
y = y_has
Where:
y_has= ../World/y (from World in has)
Equations in World
Compartment Pheromone
Initial value = 0
Rate of change = + Addition
Flow Addition
Addition = sum({Pheromone_has})
Where:
{Pheromone_has}= ../location/Pheromone (to World in has)
Variable a
a = ceil(index(1)/n)-ceil(n/2)
Where:
n= ../n
Variable b
b = index(1)-n*a-ceil(n*n/2)
Where:
n= ../n
Variable c
c = -a-b
Variable my id
my id = index(1)
Variable x
x = 50+(a-c)* 0.866
Variable y
y = 50+b* 1.5
Equations in borders
Variable x
x = off=sqrt(3/4),x+element([0,off,off,0,-off,-off],index(1))
Where:
x= ../x
Variable y
y = y+element([1, 0.5, -0.5,-1, -0.5, 0.5],index(1))
Where:
y= ../y
Equations in neighbours
Variable a
a = a+element([neighbour_offsets_a],index(1))
Where:
a= ../a
[neighbour_offsets_a]= ../../neighbour offsets a
Variable b
b = b+element([neighbour_offsets_b],index(1))
Where:
b= ../b
[neighbour_offsets_b]= ../../neighbour offsets b
Variable c
c = c+element([neighbour_offsets_c],index(1))
Where:
c= ../c
[neighbour_offsets_c]= ../../neighbour offsets c
Variable their ids
their ids = if all([a,b,c]> - (n/2)) and all([a,b,c]
This image shows the distribution of pheromone over the grid are after 3000 time units:
| Attachment | Size |
|---|---|
| 511.4 KB | |
| 2.07 KB |
