Main menu
You are here
Differential equations
At heart, many Systems Dynamics models consist of differential equations, each one represented by a compartment / flow structure, though you don’t need to know this to set up the model. On the other hand, if you’re given the differential equations, it is very straightforward to enter these into the model.
For example, given the differential equation:
dx/dt = x/20 - x2/2000
you know two things:
- there is a state variable, x, whose value changes through time; and
- the rate of change of the value of x depends only on the value of x itself.
With this information, you can deduce that it is necessary to have one compartment, labelled “x”, one flow, labelled, say “dx by dt”, and an influence arrow from the compartment to the flow.
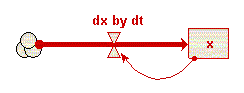
The equation can then be entered, exactly as given, into the equation dialgoue box for the flow. In Simile’s equation language, this is written “x/20-x^2/2000”. To run the model, and solve the differential equation, it is also necessary to know the initial value of x, i.e. the value at time zero. This is not given by the equation itself, but is usually reported, often described as the initial conditions. Enter this value in the equation bar (or equation dialogue box) for the compartment — in this example, “1” works well.
To complete this simulation, run the model for 200 time units, and display (plot) the values of the compartment and of the flow on separate graphs. Note that the value you enter for “dt” in the run control, by default “0.1”, is used as the time step for performing numerical integration by the Euler method. This particular equation is not very sensitive to the time step used, but if very rapid rates of change are encountered, it can be necessary to experiment with reducing the time step to find the optimum balance between speed of execution and numerical stability.
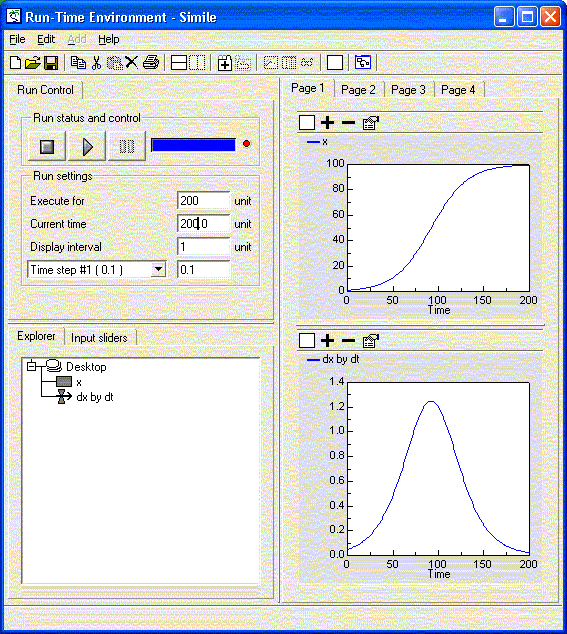
Note that in some mathematical notations, dx/dt is written as x with a dot above it, but the two mean exactly the same. Note also that the differential equation in this case can be broken into two parts, one positive contribution to the rate of change (an increase), x/20, and one negative contribution to the rate of change (a decrease), x2/2000. If this has a physical significance, two flows can be used, one flowing into the compartment and representing the positive contribution, and the other flowing out of the compartment and representing the negative contribution. Simile will automatically net the outflows off against the inflows in determining the overall rate of change.
- Printer-friendly version
- Log in or register to post comments
