Working with submodels : Association submodels
Association submodels
Association submodels are used to contain properties of relationships between one or more other submodels. If only one submodel is involved, the relationship is between different instances of the submodel. If there are two submodels, the relationships are between the instances of the two submodels. An association submodel (which looks just like a normal submodel) is used to contain elements that are held in common between the submodel instances taking part in the association. In effect, these elements do not belong to just one or other submodel but to both. For instance, the concept of a salary requires an employer paying the salary as well as the employee receiving it.
Association submodels are often used to represent a model concisely that otherwise would require repetition. If you are familiar with object-oriented programming, you will notice that association submodels are similar in concept to association classes.
For more information:
- please see the "Introduction to the association submodel concept".
- See also the 3rd video in the Simile Tutorial Series.
Terminology
A 'base submodel' is a submodel that takes part in an association.
A 'relation' is an association between instances of the same base model.
A 'role' is the arrow that connects a base submodel to an association.
To create an association submodel:
- Create one or more multiple instance submodels that will be associated, each playing a role in the association. These are the base submodels.
- Create unique identifying variables in the base submodels. The variables allow unique identification of an instance. This is easy to specify, using variables taking the value of the submodel index (or indices).
- Create a single instance submodel which will be the association submodel itself, containing variables that specify the association.
- Draw role arrows from the base submodels to the association submodel. The role arrows should be given meaningful names indicating the role the instances of the base submodel play in the association. Meaningful role names make specifying the equations in the association much easier.
- Add a condition symbol in the association submodel specifying when the association holds true. The condition is an expression involving the identity variables of the base submodels.
- Include in the association submodel all the variables that belong equally to all base submodels.
- Draw influences between relevant variables in associated submodels and the association submodel and specify these variable's equations.
To follow this in practice:
- please see the "Worked example: water flow between soil layers".
Note that there are some advanced aspects of optimising the performance of models using associations For more information please see:
In: Contents >> Working with submodels
Working with submodels : Introduction to association
Introduction to the association submodel concept
The association submodel concept in Simile represents possibly the most significant contribution that Simile has made to the field of ecological modelling. It is a very powerful concept, with two key benefits:
- it enables important aspects of the model design - the relationship between objects - to be represented in the diagram; and
- it greatly reduces the computational cost of models involving interactions between large numbers of objects of the same type, thus rendering some models tractable that otherwise would simply take too long to run.
However, it's also true that a significant amount of effort is required on the part of the modeller to understand the association submodel, and how to use it in a given situation. This is partly because the ideas involved are unfamiliar, at least in the formal, computational way needed in a modelling environment such as Simile; and partly because the ideas are difficult. However, for the modeller who deals with interactions between many objects, the effort spent in learning how to use the association submodel will be well worthwhile.
But in order to understand how to use the relational submodel in your modelling, it is important to understand why we have introduced this construct.
Why is there an association submodel concept in Simile?
Consider a model in which we decide to have two types of object: farmers and fields. There are multiple farmers, and there are multiple fields. Each farmer has dynamic attributes (such as the amount of cash they have) and each field has dynamic attributes (such as the state of crop growth or the amount of nitrogen in the soil). Clearly, in Simile terms, our model would have two multiple-instance submodels: one for the farmers, and one for the fields.
However, there are interactions between farmers and fields. The amount of grain in a field is influenced by the harvesting decision of the farmer that owns a particular field. And the cash held by a particular farmer is increased by revenue from the grain sold from each of the fields owned by that farmer. How can we handle this?
There are two ways. Let's consider the case of calculating the grain yield for each farmer. One way is for each farmer to be presented with the grain yield from all the fields, and to use only the values from the fields he owns. This can be readily done in Simile: it simply requires that the array of grain yields is multiplied by an array (also with as many elements as fields), containing 0's or 1's, with the 1's indicating that the farmer owns the field. This works fine for smallish problems, but it means that the number of operations that have to be performed is equal to n*m, where n is the number of farmers and m is the number of fields. Thus, with 1000 farmers and 5000 fields, Simile would be performing 5 million calculations every time step. This is hugely wasteful of computing time, since in fact it only needs to do 5000 (one for each field).
The other way is to pass to each farmer only the grain yield values for the fields that he himself owns. In the present example, that would be an average of 5 values per farmer - instead of 5000! These values can then simply be summed to give the total grain yield for each farmer.
The job of the association submodel is to make it possible to restrict the amount of information in this way.
Naming the components of an association
The following practise is suggested, as it results (with luck) in meaningful text being generated for the parameter names that are used in equations. These are generated by appending the name of the relevant role arrow to the name of the source component.
| Model object: | Grammatical class of Caption: | Example(s): |
| Base submodel | Noun | Farmer, field |
| Role arrow | Adjective | Owning, owned |
| Association submodel | Verb (or abstract noun) | Owns (or Ownership) |
You can also use "my" and "his" for the role arrow names when symmetry means that there aren't two distinct adjectives, as might be the case in a neighbour relationship between grid squares.
In: Contents >> Working with submodels >> Association submodels
Working with submodels : Association submodel worked example
Worked example: water flow between soil layers
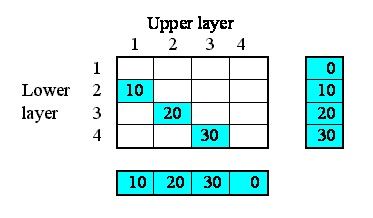
We want to model the movement of water between four soil layers. Each layer has a compartment representing the amount of water held in that layer. Water draining out of one layer will enter the layer immediately below it. The following diagram illustrates the system, with notional rates of 10, 20 and 30 units of water per unit of time flowing between the layers.
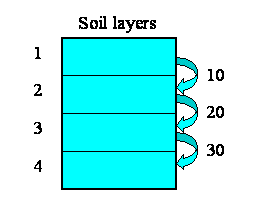
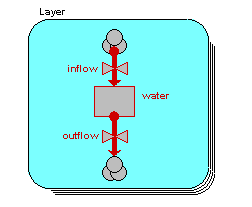
We begin by constructing a fixed-membership submodel to represent the four layers: each instance represents one layer. Each layer has a single compartment, for the amount of water in that layer. The compartment has a flow in, for the water flowing into it from the layer above, and a flow out, for the water flowing from that layer to the layer below. (There may well be other flows, but they are not relevant to the use of association submodels.) At this stage, we have not entered any values, so all the model elements are red.
Now, some of the elements have an association with each other - the relationship of one being immediately above the other.
- Layer 1 is above layer 2
- Layer 2 is above layer 3
- Layer 3 is above layer 4
But potentially there could be associations between each instance and all the other instances. In other words, the relationships that we have, in this particular system, are a subset of all the 4x4 relationships that potentially could exist. We can represent this in a matrix (below), with as many rows and columns as we have instances in our submodel.
The ticks show when the relationship of being next to exists between an upper layer and a lower layer. Note that, in this particular problem, the relationship is not symmetrical: layer 1 is above layer 2, and not the other way around. In some cases, the relationship could be symmetrical (like neighbourliness in a spatial grid), but not here.
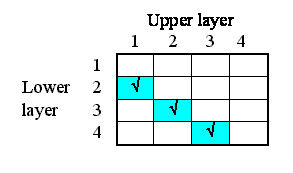
We will now modify the model diagram to represent the fact that this relationship exists between layers.
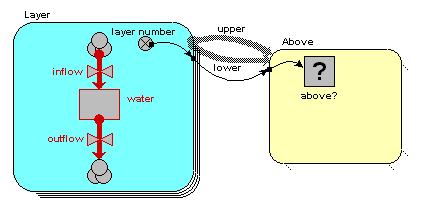
Quite a lot has happened here, so I'll explain the changes one-by-one.
layer number = index(1)
so it has a value 1 for the first layer, 2 for the second layer, and so on. i.e., as the layers go down, the index numbers go up.
above? = layer_number_upper == layer_number_lower - 1
(i.e. we are checking that the variable with the local name "layer_number_upper" is equal to the value of the variable with the local name of "layer_number_lower", minus one.) Where do the two layer_number variables come from? The answer is that they both come from the single "layer number" symbol - but one is the value of layer number for the upper layer, while the other is the value of layer number for the lower layer.
We are now in a position to pass information between pairs of instances of the "Layer" submodel. In this case, we want to pass the value for the amount of water passing out of one layer to the layer below it.
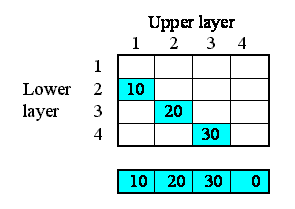
We begin by specifying how much water flows out of each layer to the layer below. Here, I've assumed 10 units per unit of time from the first layer, 20 from the second, and so on. In this particular context, this value is a property of each layer: each layer calculates the flow out of it. This could be because the flow is related to the water content of that layer, for example. We show this as a set of value beneath each column, since the columns refer to the upper layer.
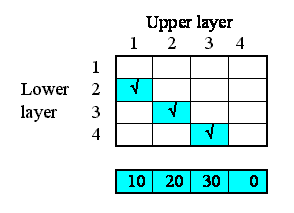
This very simple property can be specified by supplying the following equation for the flow: outflow = element([10,20,30,0],index(1)).
In terms of our model diagram, the fact that we have provided values for the four outflows simply means that the outflow arrow is now black:
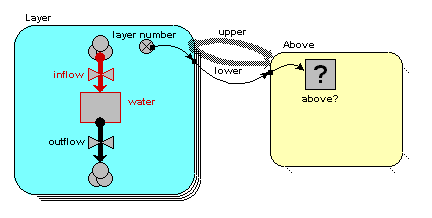
Now, each of the first three of these outflows in fact constitutes an interflow between the two layers: i.e. it is a property of the relationship between the two layers. In our matrix, we can therefore enter the values in the boxes corresponding to the linkage between the upper and lower layers:
On the model diagram, we add a variable inside the "Above" submodel, here called "interflow", and take an influence arrow to it from "outflow". This shows that (in this particular model) the interflow is calculated from the each soil layer's outflow.
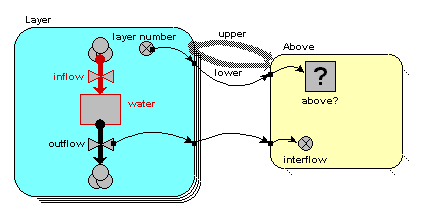
Because we are inside the "Above" association submodel, we could (potentially) set interflow to the outflow from the upper layer or the outflow from the lower layer. The first has the local name "outflow_upper" in the equation dialogue box, while the second has the local name "outflow_lower". In this particular model, we want it to be from the upper layer, so we set the equation to: interflow = outflow_upper.
However, we know that the interflow between layers becomes the inflow for the lower layer. In our matrix, we show this fact by copying the interflow values across to the right, to the column representing the inflow into each layer.
In the model diagram, we draw an influence arrow from the "interflow" variable in the "Above" submodel to the "inflow" variable in the "Layer" submodel.
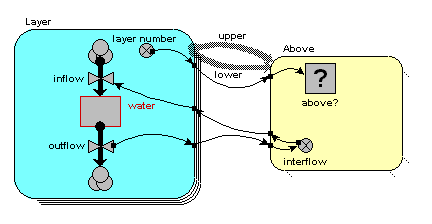
When we look inside the equation dialogue window for inflow, we get a bit of a surprise. We expect to see interflow as an influencing variable, but:
- we actually see it offered twice, with local names "interflow_lower" and "interflow_upper"; and
- each of these is a list (i.e. {interflow_lower} and {interflow_upper}), rather than a normal variable.
It's offered twice, because we could (potentially) be interested in the interflow values relating to the upper layer (those under the columns in the matrix above); or the interflows relating to the lower layer (the interflows to the right of the rows in the matrix above). We want the latter, so we choose {interflow_lower}.
Why is the information from the submodel a list rather than a scalar variable? Well, potentially there could be as many values as there are soil layers. In this particular case, we happen to have put in a condition that restricts it to one value for three of the layers, and none at all for one layer, so our list will contain only zero or one value, depending on the layer. But if we had allowed water to flow directly to a layer from any layer above it, then the list could contain several values.
Anyway, the fact that it's in a list means that we have to convert it to a single value by summing up the elements of this list. So the actual equation we use for inflow is:
inflow = sum({interflow_lower})
The model now only requires initial values for the water compartment to make it runnable. On running it, you will note that water in each of the top three layers decreases by 10 per time unit, as this is the amount by which the outflow is greater than the inflow. The water in the bottom layer increases by 30 per time unit, because its outflow is zero.
In: Contents >> Working with submodels >> Association submodels
Working with submodels : Role properties dialogue
Role properties dialogue
There are two advanced properties of role arrows that are set using this dialogue box. Note that it is not normally necessary or desirable to set these properties. They allow the program generation routines to make certain assumptions. If these assumptions are not valid, chaos will result.
Exclusive role
An exclusive role is one such as motherhood. Although each mother may have many children, each child has (or at some point had) exactly one mother. This is often expressed as a one-to-many relationship.
If you know there is always exactly one element in the list returned from the association submodel to the base model in this role, then you may (but do not need to) check the "Exclusive role" check box. The single element will then be returned by itself, without being enclosed in a list as would otherwise be the case. Note that in the aforementioned case of a motherhood relation, it would be the "is_child" role that is marked as exclusive, since the base model with the "child" role is getting the values from the unique association with a mother.
This allows you to use the value as an argument to functions such as element(). It may also be necessary to use this in conjunction with the property of influence arrows: "Use values made in same time step". It would probably help to talk about your model on the forum.
Allow base instance lookup
If you want to use one-sided relation enumeration, then the base model whose index you are looking up (as you loop over the instances of the other base model) has to be the one whose index is referred to as index(1) in the relation model. By default this would be the one with the role arrow that you added most recently, but it can be set using this property on its role arrow.
Since only one base model index can correspond to index(1) in the association submodel, setting this property on one role arrow clears it from other role arrows going to the same association submodel.
Setting this property never does any harm, and has other uses: if for some reason you have to delete one of your base models then re-create it, Simile might decide to change the order in which it assigns the index values in the association submodel, so what was previously index(1) becomes index(2). For this reason it's better to set variables in the base models to their indices and have influences from these into the association model (it also makes the equation more readable), but if you have referred directly to base model indices, setting this property allows you to control which base model index gets used as index(1).
Comments
Free-form comments can be entered in this text box, and are stored with the model. You are encouraged to comment your role arrows at length, so if you have used them wrongly, someone else can figure out how to put them right.
In: Contents >> Working with submodels >> Association submodels
Working with submodels : One-sided relationship enumeration
One-sided relationship enumeration
One-sided relationship enumeration, also known as base instance lookup, is a feature that makes it quicker to create associations between submodels with large numbers of instances. The problem is that when creating an association, Simile would normally loop over instances of one of the base submodels, and for each instance, loop over the instances of the other, checking the existence condition of the association for each possible pairing of base models. This means that if one base model has n instances and the other m, the number of checks that must be made is nxm, potentially a very large number. Base instance lookup can be used if there is sufficient data in the instances of one base submodel to calculate the indices of the instance(s) of the other base model with which it will be associated. For this to be the case, the association must be independent of the actual values in one of the submodels (except those that can be derived from its index, e.g., physical location of a grid square). It can of course be used in self-associations, where the same submodel serves as base model on both sides of the association.
To illustrate the technique, we will discuss the case of using it specifically to make more efficient the creation of large rasters. A raster is a grid of pixels. Each pixel is equivalent in size and shape. Usually, each pixel is square, though it is also possible to work with other rasters. In this discussion, we shall consider only square grids. Note that Simile version 6.1 introduces a feature that allows a raster to have a built-in neighbour relationship without any need for an association submodel, and that this feature internally uses something like base instance lookup to create this relationship.
Square grid example
In a square grid, each pixel has potentially eight neighbours: north-west, north, north-east, west, east, south-west, south and south-east. However, pixels at the edge of the grid will have only a subset of those neighbours. For example a pixel on the northern edge of the grid will have five neighbours (west, east, south-west, south, and south-west) and one in the south-west corner will have only three: (north, north-east and east).
To take advantage of the powerful features in Simile, we represent the pixels as instances of a multiple-instance submodel. The number of instances is equal to the width of the grid (in pixels) multiplied by the height. Each pixel has an id number, equal to the index of its position. The row and column that the pixel is in can be calculated from the id number, knowing the width of the grid.
Within each pixel, we can create an eight-instance submodel representing each possible neighbour. To allow for edge effects, we can make the existence of each of the eight conditional. Each (possible) neighbour-instance has a row and column calculated from its position relative to its parent pixel. Now each pixel has access to a list of its neighbours.
To use this knowledge, we can create an association submodel, representing the relationship of "neighbourhood" between the central pixel and the (up to) eight pixels that border it. Two role arrows are drawn between the pixel submodel and the neighbourhood submodel, representing the pixel in the centre and the pixels in the border.
The final step is to create a condition in the neighbourhood model that evaluates for each pixel whether any given pixel is in the neighbourhood. Since each pixel has a list of its own neighbours, this condition is simply:
any(my_id_border == {neighbours_ids_centre} )
In this expression, neighbours_ids_centre is the list of ids of neighbours from the instance in the "centre" role, and my_id_border is the index of the pixel that is potentially in the border (set to index(1) in a variable inside the grid square submodel). The condition is true (and the relationship therefore exists) for a centre and a border pixel, if any of the elements of the list of the neighbour_ids in the centre equates to the index of the pixel in the border.
So far, it is important to emphasise that we have followed the procedure that is standard in Simile for many different types of relationship. We now need to look carefully at what this model represents, how Simile is converting it into a computer program, and how it can be changed to make it more efficient.
What does the model represent?
This model looks unusual as the condition for the relation uses values from a submodel of the base model. But the operation is pretty similar to the self-relation in the previous section, with the difference that each base model instance can be in relation with many other instances. Any time the index of the instance in the "border" role matches any of the indices from the "neighbours" submodel of the instance in the "centre" role, an association instance will be created. Now if the "centre" instance needs to have information from all the "border" instances, this can be passed to the association via the "border" role and back via the "centre" role. Because different instances have different numbers of "neighbours" submodels, they have different numbers of associations.
How is Simile running it?
Now for the bad news. When Simile creates a program for any association submodel, it first creates nested loops for each of the base models. If there are two role arrows from the same base model as in this case, it will loop through all its instances, and for each one, loop through all its instances again. This is so it can compare values from every instance with those from every other instance, in order to decide which pairs the association holds between. In this model there is yet another loop inside these -- it has to loop through the instances of "neighbours" in the "centre" role to see if any match the index of the square in the "border" role.
This only has to be done when the model is initialized, as the definition of the relationship clearly dos not change over time or from run to run. Once the relationship is created, the association submodel instances have pointers to their base instances so they remember which ones to use. But if there are, say, a million grid squares (not an excessive number for Simile) it takes 8x1012 comparisons to set up the relationship, which would keep your computer busy for hours. So what can we do?
How can we improve efficiency?
Very easily, just get rid of the association submodel, and instead have any variable that needs to be shared between neighbours taken outside the grid square submodel into an array variable of its own. Then draw an influence from that array to a variable in the "neighbours" submodel, and give it the equation element([array_outside],neighbours_ids). The values of this variable can then be summed inside the grid square but outside the "neighbours" submodel to give the sum of the original values from all an individual's neighbours. This only needs one level of looping through the grid square model, since it is using the neighbours_ids values directly to index the array rather than comparing them with those from other instances.
But this model is not as clear as one with an explicit neighbour relationship, especially if many values are passed between neighbours. So we have added a feature to the interpretation of the condition symbol that allows an association to be built in a similar manner, i.e., by using the index to look up one of the base instances rather than seaching through all of them and comparing their indices with a value we got from the first base instance. To do this, we rewrite the condition's equation like this:
any(index(1) is {neighbours_ids_centre} )
Previously, this expression would have been written with the equality operator "==", instead of the key word "is". The new key word has been introduced in order to invoke the efficient program generation that is possible for rasters. Note that we have also replaced the reference to the variable my_id in the submodel with the "border" role, with the function index(1). This is because index(1) means the same thing (because we set "Allow base instance lookup" in the properties dialogue of the "border" role arrow), and we cannot use a variable from the base model in that role until we have looked up the base instance itself.
This is not the only situation that is applicable: in general, as the name implies, the feature is useful for any situation where the relationship can be calculated in a loop over only ONE of the roles. In this case, because each pixel is able to calculate its own list of neighbours, it is not necessary to take each possible pair of pixels and determine if they are neighbours. It is from this short cut that the improvement in efficiency stems.
There is a model in the catalogue on Simulistics web site, showing all this in practice. If, without looking at the example, you could create an equivalent model, you are a graduate summa cum laude of Simile use. The example can be used as a starting-point for most work on rasters, grid squares and so on.
Variable-membership base models
In the original implementation, it was not possible to set an association model's membership by base instance lookup if the base instance was itself variable-membership. This was because a variable-membership submodel is implemented as a linked list of data structures, and the only way to find a member with a particular index is to search sequentially through the list. This is the normal way of setting up an association, so in the case of a one-to-one or many-to-one association, having a special construct would not improve efficiency.
However, in Simile v6.1 we have extended the element() function to select sublists from lists. This it does by going through the list sequentially, and returning values as it find indices that match the elements of the second argument (which therefore need to be in ascending order). So, we can do something similar when building a many-to-many association. If the submodel on one side can generate an array or list of index values for a variable-membership submodel on the other side (possibly the same submodel) these can now all be looked up in a single pass by using the 'any(...)' construct described above.
Having implemented this, we found that one-sided enumeration is quite a lot faster than checking every combination of base models even in the case of a one-to-one relationship involving a variable-membership base model. This is partly because searching for a single index value can be stopped as soon as it is found, but mostly because a lot less pointer arithmetic is required just to check an index than to actually get values from the model and plug them into the existence condition equation. So, using 'index(1) is...' is now also recommended for variable-membership base submodels.
Looking up instances by multiple indices
Another small change in Simile v6.1 is to allow more than one index to be specified when looking up a base submodel instance. The indices must be specified in descending order (i.e., outermost first) and joined by 'and', e.g.,
index(2) is y and index(1) is x
or
any(index(2) is {list_of_y} and index(1) is {matching_list_of_x})This will work when looking up instances of fixed or variable membership base submodels, but the number of indices specified must be exactly the number of indices that the base submodel has. This capability has been added to make it possible to look up instances of the new special-purpose submodels.
In: Contents >> Working with submodels >> Association submodels