Graphical modelling in Simile
Simile's graphical language supports three different but overlapping modelling concepts:
- System dynamics
- Discrete event based
- Object- or agent-based
System dynamics allows a system to be represented as quantities of real or abstract materials in reservoirs (compartments), moving continuously between them via a network of flows with rates derived from the state of the system. It is at the heart of Simile, and the diagram components that underlie it are used in all Simile's modelling concepts. If you are new to computer modelling, you should familiarize yourself with the system dynamics approach first.
Discrete event based modelling (new to Simile v6) allows instantaneous changes in a system's state to occur at arbitrary times. Event occurrences can be scheduled in advance, or triggered by model values crossing thresholds, or by other events, possibly after a delay. In pure event-based modelling, there is no regular time step and the state of the model does not change between events. Simile allows continuous change and discrete events in the same model.
Object- or agent-based modelling allows a single template for a functional unit in the model (known as a 'class') to work as many actual units (known as 'instances' or 'individuals') in the model. In Simile, instances can be permanent or can be created and destroyed as the model runs. Relations between instances can be specified, allowing influences to work between particular pairs of instances of the same or different classes.
Graphical Modelling in Simile : System Dynamics
System Dynamics modelling in Simile
A model is made up of compartments, representing quantities of material, and flows, representing movements between compartments. Where material moves in or out of the area of interest, a flow ends in a cloud. A flow has a bowtie, representing a valve or pump that sets its rate. Flows are calculated from compartment levels, and variables can be used for intermediate results, for constants, or for getting data into or our of the model. Influences indicate which component values affect which others.
See also the 1st video in the Simile Tutorial Series.
|
|
An amount of some substance |
|
|
|
A process moving a substance between compartments |
|
|
|
A constant or variable quantity |
|
|
|
Represents the fact that one quantity is used to calculate another |
Model diagram elements : Compartment
 Compartment
Compartment
How to add a Compartment symbol
See Adding node-type elements. Note that you can add a compartment on top of a cloud, in which case the cloud becomes a compartment.
Interpretation
The compartment symbol is used to represent a quantitative state variable. Notionally, we think of a compartment as containing an amount of some substance, though it can be used in other situations where we want to represent the concept of state.
The informal interpretation of a compartment in System Dynamics modelling is that it represents a real, physical compartment that can contain some substance, just like a tank holds water. The compartment requires to be given an initial value - how much water does the tank hold at the start of the simulation? - and we need to construct flows in and out of the compartment so that the amount it holds can change over time.
This interpretation is fine to begin with, but must not be taken too literally. A compartment in System Dynamics modelling is, mathematically-speaking, a state variable: i.e. it is a variable whose behaviour is described by a differential (or difference) equation. And, unlike real, physical compartments, a compartment in System Dynamics:
- can go negative (if the flows out are greater than the flows in, when the compartment gets to zero);
- has infinite capacity (can go on increasing indefinitely);
- cannot contain multiple substances. A real tank can contain both water and oil, but in System Dynamics modelling we would need a separate compartment for each one. However Simile allows a compartment to be an array with the dimensions of an enumerated type -- this could be used to model a single tank containing multiple substances.
- can represent some state that does not correspond to the amount of a substance (such as the height of a tree, the area of land, the time when some event happened, or the x co-ordinate of a moving object).
Rules
- You should not draw an influence arrow to a compartment, except for the special case of initialising it from other model variables. The behaviour of a compartment is determined solely by the net flows in and out of it. Its value at any point of time is found by incrementing or decrementing its value from the previous time step with the net inflow. But when you draw an influence arrow to a model element, you are saying that its value is calculated directly from the influencing variable, and that is incompatible with an approach base on adding or subtracting something from its previous value.
- If you do draw one or more influence arrows to a compartment to initialise it in terms of other model variables, then those variables should be static (i.e. not time-varying).
- If two compartments are connected by a flow arrow, then the two compartments should represent the same substance, and should have the same units.
In : Contents >> Graphical Modelling >> System Dynamics
Model diagram elements : Flow arrow
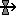 Flow arrow
Flow arrow
How to add a Flow arrow
See Adding arrow-type elements.
Interpretation
The flow arrow is used to specify a term contributing to the rate of change of a compartment. If the flow arrow enters a compartment, it specifies a positive contribution to the rate of change of that compartment. If it leaves the compartment, it specifies a negative contribution to the rate of change.
The information on the flows entering and leaving each compartment is used to calculate the net rate of change of the compartment. The net rate of change is the sum of all the inflow values minus the sum of all the outflow values. The net rate of change is in turn used to calculate the change in the value of the compartment.
If your model needs to keep track of changes in the amount of a substance but you are not interested in where it comes from or goes to, your flow may start or finish on a blank part of the model diagram. In this case a "cloud" will be drawn at the end point, indicating that the amount of substance there plays no role in the model. Each cloud may only have one flow connected to it.
Influences to and from a flow are attached to a "bowtie" (or "valve") symbol which is positioned on the flow. This represents the point that controls the rate of the flow.
In most respects, a flow is treated just like a variable. You can use the full range of the equation language when you enter an equation for the flow, just as you can do for a variable. You can have influence arrows going from it to other parts of the model, again just like a variable. The two differences are that:
- a flow is the only way you can express a rate of change term for a compartment; and
- a flow cannot be a "file parameter".
Rules
- A flow arrow can only be drawn into and/or out of a compartment.
- Influence arrows can be drawn to and from flows.
- The units for a flow value must be the units of the corresponding compartment(s) that it is linked to, per unit of time. For example, if you have a flow going into a compartment whose units are kg, and the unit of time for the model is a year, then the units for the flow must be kg/year.
- It is quite legitimate to have an influence arrow going from one flow to another. You might wish to do this if one flow is proportional to another, or if the two flows are in different submodels.
In : Contents >> Graphical Modelling >> System Dynamics
Model diagram elements : Variable
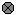 Variable
Variable
How to add a Variable symbol
See Adding node-type elements.
Interpretation
A variable is used to hold one or more values. The value or values come from a mathematical expression. The expression may simply be a number, or it may be a complex mathematical expression involving various variables, operators (such as + and -), functions (such as log or square root), and conditional elements. The value of a variable may vary during the course of a simulation, if it is calculated from other parts of the model that change over time, or it may be constant.
The term "variable" is used to refer to a specific type of model element. This single element can be used for a wide variety of purposes, each of which is referred to in a different way by some modellers. There is rich potential for confusion here, so the following table sets out the correspondence between how a Simile variable is used in a model, and how a modeller would interpret that use. (In case you are wondering why we don't have a number of model elements, one for each type of use: the answer is that this would lead to an unnecessary proliferation of element types. Also, you might wish to change the role of a variable as you build up a model, and you would not want to have to keep on deleting one symbol and replacing it by another.)
|
Modelling use |
Set-up of "variable" |
|
|
No influence arrows pointing to it. One or more influence arrows pointing from it. Value is a numeric constant or value is not supplied and "Fixed parameter" radio button is selected. |
|
|
No influence arrows pointing to it. One or more influence arrows pointing from it. Value is a numeric constant (representing initial slider position). "Variable parameter" radio button is selected. |
|
Exogenous variable: this is a variable whose value changes during a simulation run, and which influences the value of other variables, but which is not itself influenced by other variables. Typically used for climatic inputs, such as temperature or rainfall. |
No influence arrows pointing to it. One or more influence arrows pointing from it. Value is some function of simulation time (i.e. involves the built-in function time). |
|
Intermediate variable, also referred to as a derived variable |
One or more influence arrows pointing to it. One or more influence arrows pointing from it Value is a function of the variables influencing it and also possibly of model properties such as current time |
|
Output variable: typically, this is used to report on some aspect of model behaviour (e.g. the ratio of two compartments). |
No influence arrows pointing from it. Otherwise as intermediate variable |
|
Attribute of an object: there is only sense in doing this if the variable is inside a multiple-instance submodel, with different instances having different values. E.g. the x-coordinate or the species type of each of many trees. |
No influence arrows pointing to it. No influence arrows pointing from it. |
Rules
- A variable symbol may have zero or more influence arrows pointing to it.
- A variable cannot have influence arrows pointing to it if it is a "file parameter".
- A variable symbol may have zero or more influence arrows pointing from it.
- A variable may not have other kinds of arrow pointing to or from it.
In : Contents >> Graphical Modelling >> System Dynamics
Model diagram elements : Influence arrow
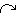 Influence arrow
Influence arrow
How to add an Influence arrow
See Adding arrow-type elements.
Interpretation
To say that "A influences B" (i.e. to draw an influence arrow from A to B) means that A is used to calculate a value for B: in other words, the equation for calculating B will include A.
Rules
You can drag an influence arrow from and to most model elements. The exceptions and special cases are noted here below. Note that if you try to drag an influence arrow to a model element that cannot receive one, then it turns blue instead of green, and you will not be able to connect them together. You can store comments associated with an influence arrow by double-clicking the arrow.
 Compartments
Compartments
- Elements that influence a compartment are used only to calculate the initial value of the compartment. Thereafter, the value of the compartment is calculated by adding the flows in and subtracting the flows out. It is not common therefore to draw an influence arrow to a compartment, though it is possible (in order to calculate the initial value). For example, although one may informally say "water temperature influences fish population size", in the model, temperature must actually influence one of the processes (reproduction, death and so forth) which change the fish population size. The influence arrow from the temperature variable must therefore point to one (or more) of the flows in or out , and not to the compartment representing fish population size itself.
 Submodels
Submodels
- When working with submodels, you may find that an input parameter (A) in one submodel actually corresponds to a variable (B) in another, especially when the two submodels were developed separately, then later brought together. In order to get rid of the duplication, draw an influence arrow from B to the influence arrow from A. This is the only circumstance in which it is possible to draw one influence arrow pointing to another. Input parameter A will disappear, and the influence arrows will be re-drawn to show B directly influencing the element previously influenced by A.
- You can drag an influence arrow to a submodel boundary, from either inside or outside the submodel. This has no meaningful modelling function, but acts as a temporary placeholder to the influence arrow until it is connected to an element on the other side of the boundary. In order to do this, drag an influence arrow from the head of the existing arrow to the desired element.
- You cannot drag an influence arrow from a submodel boundary, other than to complete an influence arrow drawn to the submodel boundary (as described in the previous bullet point).
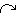 Influence and
Influence and  role arrows
role arrows
- You cannot drag an influence to a role arrow or to another influence arrow.
- If an influence shares part of its route with one or more role arrows (in either direction), then the normal interpretation is that the values it supplies will only be those from the base model instances in the corresponding roles, or from the association model instances for which the instance containing the destination is in the appropriate role. The different interpretations are selected by prefixing the caption of the source component (or suffixing if going from association to base) with the caption of the relevant role. As of Simile v6, the interpretations can be enabled or disabled by checkboxes in the influence properties dialogue. Also the interpretation that would apply if the role arrow were not present, i.e., get values from all source model instances, is also available and can also be enabled or disabled.
- In Simile v6.1, an alternative interpretation is provided for influences within multiple-instance submodels -- the ability to get values from all instances, as if the destination were outside the submodel, rather than just from the current instance. Furthermore, for influences within special-purpose submodels, there are interpretations that provide values from just a special subset of other instances, e.g., neighbour instances. Again, any of these (as well as the default interpretation) can be enabled or disabled from the properties dialogue.
- If an interpretation is enabled that gets values from other instances than the current one, the influence arrow will be decorated with an oblique stack that it passes through, indicating that it carries values between different instances of its submodel.
- To invoke the property dialogue box for an influence arrow, double-click on the arrow, or right-click on it and select "Properties..." from the context menu.
 Calculation order
Calculation order
An influence arrow indicates that the value of one component is used in calculating the value of another. So it puts a constraint on the order in which the two values can be calculated each time step; the one at the head must be done after the one at the tail.
This means that if it is possible to get from a model component around a loop of influence arrows back to the same component, the model cannot be executed, because no ordering of the calculations can satisfy all the constraints. The problem is called circularity. Usually this problem indicates that a certain variable in the model should in fact be a compartment, and an influence that connects to it should instead connect to a flow going to it. But there are some circumstances in which circular influences are OK.
- Influence arrows have one further property that can be set. The property is "Use values made in same time step". The property indicates how the ambiguity associated with a circular loop of influences is to be resolved.
- Normally, the value of the component at the end of an influence is calculated after that at its start in each time step. Selecting "Use values..." removes this constraint, and shows this by drawing the arrow dashed instead of solid.
- This may be used in combination with the iteration symbol to implement many iterative methods.
- You can also use this property to create a model process that iterates a fixed number of times and stores all its intermediate results in an array. In this case you do not need the iteration symbol. If you have two components in different fixed-membership submodels, and each has the same number of instances, then they can each have an influence to the other provided one of the influences has the "Use values made in same time step" property, and the equation of the component at the end of this influence uses only values of the other component with indices lower than its own. Subject to a similar restriction it is also possible to specify iteration between a base submodel and its association submodels.
There are two functions in the equation language, "last()" and "sofar()", which also allow a model with a circular chain of influences to execute. Putting "last()" around an expression means that its value at the end of the last time step is to be used, so the component using it does not have to be evaluated after it each time step. Putting "sofar()" round a value has the same effect as selecting the "Use values..." property described above for the influences used by that value; it is used to resolve circularity problems involving intermediate variables, where there is no influence arrow on which the property could be set.
In : Contents >> Graphical Modelling >> System Dynamics
Graphical Modelling in Simile : Discrete event based
Event-based modelling in Simile
A pure discrete-event-based model includes only event symbols (time series and derived/delayed) and states. An event symbol only has a value at the point in time at which it occurs. The value of a derived event occurrence is calculated by its equation, which can include the value of the triggering event occurrence. A state has a rule for each event symbol that influences it. When an influencing event occurs, the state's new value is given by the corresponding rule, otherwise it stays the same.
A model that mixes system dynamics (continuous) and discrete-event based operation also includes limit event symbols and squirts. A limit event occurrence is triggered when its equation reaches its minimum or maximum value, allowing continuous processes to set off events. A squirt is a derived event which causes an instantaneous transfer of material between compartments, allowing events to affect continuous processes. State changes can also affect continuous processes, but only squirts can cause discontinuities in the values of compartments.
See also the 5th video in the Simile Tutorial Series.
|
|
An instantaneous occurrence which can have a magnitude |
|
|
|
A quantity set by events according to rules |
|
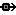 |
squirt | An instantaneous transfer of a substance between compartments |
 |
If an influence originates from a discrete event valued component, it is shown 'bulged' to indicate that it carries a discrete event value. Such an influence cannot terminate on a continuous-valued component. | |
|
|
The channel components which specify changes to the membership of population submodels can be either continuous or discrete valued. If one or more discrete valued influence terminates on one of these, it is discrete valued and behaves like a squirt component, adding or removing as many submodel members immediately as the continuous version would over one time unit. |
|
|
|
||
|
|
||
In: Contents >> Graphical Modelling
Discrete event-based modelling : Event element
 Event
Event
How to add an Event symbol
See Adding node-type elements.
Interpretation
An event symbol represents something that happens at an instant in time, such as the arrival of a package. The event represented by a symbol may occur any number of times during a model run, or not at all. An event occurrence can have a numerical magnitude, and having a magnitude of zero is the same as not occurring. The effects of an event occurrence can be proportional to its magnitude. Alternatively it can be boolean, i.e., all-or-nothing. Event symbols should not have array equations, but can go in multi-instance submodels, in which case the event can occur independently in each instance of the submodel.
In system-dynamics models, time advances by regular steps. When an event is about to occur, Simile will execute a time step with a size that will advance the time to exactly the point at which the event is predicted to occur, in order that the effects of changes made by the event are not subject to time step rounding errors.
There are three types of event, which differ in how they are triggered. The equation dialogue for an event includes radio buttons to select between these event types, and they are distinguished by different 'decorations' on the event symbol in the model diagram.
|
Modelling use |
Set-up of "event" |
|
The exact time at which the event occurs is determined by extrapolation of the equation value over the previous system-dynamics time step. If the integration method is Euler, linear extrapolation is used; if Runge-Kutta, it is done by a quadratic approximation. If adaptive step-size variation is selected, a check is done that the crossing actually occurs around the predicted time, and the time step is re-calculated with a new prediction if the difference is too great. |
Only has inflluence arrows from continuous valued components One or more influence arrows pointing from it to other events, squirts or states Magnitude is on/off if one limit supplied, integer of -1 or 1 if both limits supplied |
|
If a time series event symbol is put inside a multi-instance submodel, the values in the series must be arrays with the dimensions of the submodel. At each time point in the series, the event will occur in all instances of the submodel for which the corresponding array element is non-zero (or 'true' if type is boolean). |
No influence arrows pointing to it. One or more influence arrows pointing from it to other events, squirts or states. Occurrence times and magnitudes given by series data |
 Derived event (No decorations): This is an event that occurs as a result of other event occurrences. It must have an influence from at least one other event or squirt, and may occur whenever any of them occur. It may also have influences from other components, whose values may be used in its equation. Its equation is evaluated when it is triggered, and gives its magnitude. The equation cannot refer to event values directly, but can include the special function 'trigger_magnitude()' which gives the magnitude of the triggering event, or their sum if more than one happens simultaneously. If the trigger magnitudes sum to zero, or the equation evaluates to zero (or 'false' if type is boolean) the event will not occur. Derived event (No decorations): This is an event that occurs as a result of other event occurrences. It must have an influence from at least one other event or squirt, and may occur whenever any of them occur. It may also have influences from other components, whose values may be used in its equation. Its equation is evaluated when it is triggered, and gives its magnitude. The equation cannot refer to event values directly, but can include the special function 'trigger_magnitude()' which gives the magnitude of the triggering event, or their sum if more than one happens simultaneously. If the trigger magnitudes sum to zero, or the equation evaluates to zero (or 'false' if type is boolean) the event will not occur.The equation of a derived event can be of the form after(t,x) where t and x are subexpressions. In this case the magnitude of the event is x at the time of triggering, but it does not occur until t time units later. This is the only context in which after(...) can be used. |
Must have an influence from at least one other event or squirt, can have other influences to it One or more influence arrows pointing from it to other events, squirts or states. |
In: Contents >> Graphical Modelling >> Discrete-event based
Discrete event-based modelling : Squirt arrow
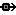 Squirt arrow
Squirt arrow
How to add a Squirt arrow
See Adding arrow-type elements.
Interpretation
The squirt arrow is used to specify where event occurrences cause sudden changes to the value of a compartment. If the squirt arrow enters a compartment, it specifies a positive step change to that compartment. If it leaves the compartment, it specifies a negative step change (unless the magnitude of the squirt occurrence is negative in which case these directions are reversed, as for a negative flow value). Many aspects of using squirts are similar to using flows.
If your model needs to keep track of changes in the amount of a substance but you are not interested in where it comes from or goes to, your squirt arrow may start or finish on a blank part of the model diagram. In this case a "cloud" will be drawn at the end point, indicating that the amount of substance there plays no role in the model. Each cloud may only have one flow or squirt connected to it.
Influences to and from a squirt arrow are attached to a "target" (or "bulb") symbol which is positioned on the squirt arrow. This represents the point that generates the transfer. Influences from a squirt arrow start from this point and are used in the same way as those from an event symbol, and must go to other squirts, events or states.
In most respects, a squirt is treated just like a derived event. You can use the full range of the equation language when you enter an equation for the squirt, including the trigger_magnitude() and after() functions, just as you can do for a derived event. The two differences are that:
- a squirt is the only way you can express an instantaneous change term for a compartment; and
- a squirt cannot be a time series event or a limit event.
Rules
- A squirt arrow can only be drawn into and/or out of a compartment.
- Influences can be drawn to a squirt's bulb, and must include one from another squirt or event symbol.
- Influences can be drawn from a squirt's bulb to other squirts, events or states.
- The units for a squirt value must be of the same dimensions as the units of the corresponding compartment(s) that it is linked to. For example, if you have a squirt going into a compartment whose units are kg, and the unit of time for the model is a year, then the units for the squirt can be kg, g, lb etc. An automatic conversion will be performed if necessary. The time units do not matter (unlike flow units) because the transfer is instantaneous.
In: Contents >> Graphical Modelling >> Discrete-event based
Discrete event-based modelling : State element
 State
State
How to add a State symbol
See Adding node-type elements.
Interpretation
A state is a model value that is changed by events, but otherwise stays the same. A state does not have a unique equation, but rather a set of rules, each consisting of an event (the trigger) matched with an equation (the effect). There will be one rule for each event that influences the state, plus an extra effect labelled "reset..." that sets the initial value of the state when the model resets (or when a new instance of the state's parent submodel is created).
In the equation dialogue for a state, the influencing event symbol captions (and reset...) are listed to the left of the equation field, and clicking on an event caption shows the effect for an occurrence of that event. In the equation bar, a pull-down menu to the left selects the caption of the event whose effect is to be edited. The popup text for the state is a condensed form of the rules, e.g., "9 on event1, 6 on event2, 0 on reset."
Components with continuous values can also influence the state, and their values can be used in one or more of its effect equations.
The value of a state after an event occurrence depends only on the effect equation of that event, and not on its previous value. However the equation can use the prev(0) function to refer to the state's previous value if the new value is to be a function of it. The equation can also use the trigger_magnitude() function to refer to the magnitude of the triggering event occurrence if this is to affect the state's new value. The effect equations cannot use the after(t,x) function; the state's value always changes immediately after the triggering event occurs.
Currently the order in which the rules are applied if multiple triggerring events occur simultaneously is undefined.
Rules
- A state must have influences from at least one event or squirt symbol
- A state must have an equation for each event or squirt symbol influencing it, plus one for reset
- Other components (including other states) can influence it, and their values can be used in its equations
- All of its equations must evaluate to quantities with the same units and dimensions
- A state can influence any other component
In: Contents >> Graphical Modelling >> Discrete-event based
Graphical Modelling in Simile : Object- or agent-based
Object- or agent-based modelling in Simile
A submodel is a distinct group of components in a model, and can represent a class. Submodels with specified dimensions have a fixed number of potential instances. Population submodels represent groups of individuals who appear, move, reproduce and disappear according to the four process or channel symbols -- creation, immigration, reproduction and loss.
A role arrow causes the submodel at the head to have an instance or group of instances for each instance of that at its tail, as if it were nested inside. Each role arrow multiplies the potential number of instances of the submodel at its head. This can contain condition symbols, which allow the existence of each instance to be turned on or off.
The alarm symbol indicates that when the model values are updated, the components in its submodel should be evaluated repeatedly until the alarm's test condition is met. Condition and alarm symbols have slightly different effects when influenced by events. A conditional submodel only exists at the point at which the triggering event occurs, while an alarm submodel's components are only re-evaluated (but maybe many times) when the triggering event occurs, and keep the same values at other times.
|
|
An envelope enclosing a group of model elements, collectively representing a class of object |
|
|
|
A process creating the initial number of instances of a population submodel |
|
|
|
A process creating new instances of a population submodel |
|
|
|
A process creating new instances of a population submodel for each existing instance |
|
|
|
A process destroying instances of a population submodel |
|
|
|
Represents the fact that one object is associated with another, with each playing a role in the association |
|
|
|
Represents the fact that an instance of a submodel can exist only under specific conditions |
|
|
|
Represents an iterative loop within a single time-step |
In: Contents >> Graphical Modelling
Model diagram elements : Submodel
 Submodel
Submodel
How to add a submodel symbol:
See Adding Submodels
A submodel is first and foremost a way of grouping together a number of other model elements, including other submodels. This is done by either drawing a  submodel envelope around a number of elements in the model diagram, or by creating an empty submodel and inserting model elements into it.
submodel envelope around a number of elements in the model diagram, or by creating an empty submodel and inserting model elements into it.
However, the reasons for wanting to do this are many and varied, and it is important to appreciate that the submodel construct can be used for a range of modelling needs. There are considerable benefits to using a single method to fulfil this range of needs, both in reducing what you need to learn, and keeping the resulting models simple and flexible.
This section overviews the different uses of the submodel construct, and the different types of submodel that you can have. Other sections provide more detail on particular topics.
Using a submodel to show the main components of a complex model
You have constructed a model with a number of compartments and flows. Some relate to vegetation; some to the animals in the area; some to soil water and nutrients. By grouping the model-diagram elements for these different parts into submodels (called "Vegetation", "Animals" and "Soil"), the gross structure of the model is immediately apparent.
Conversely, you may prefer to design a model in a top-down fashion. Starting with a blank screen, you can rapidly add submodels corresponding to the main components of a proposed model, then subsequently add the various compartments, flows etc inside these.
Using a submodel for multiple views on a model, perhaps at different scales
Once part of a model is made into a submodel, you can open a separate window for it (by double-clicking on its boundary with the  pointer). This window can be kept on the screen while you scroll the main model diagram to some other part of the model. Also, you can change the zoom factor for each main model window or submodel window separately, enabling you to see part of the model in fine detail while maintaining an overview of the whole model at a coarser scale.
pointer). This window can be kept on the screen while you scroll the main model diagram to some other part of the model. Also, you can change the zoom factor for each main model window or submodel window separately, enabling you to see part of the model in fine detail while maintaining an overview of the whole model at a coarser scale.
Using a submodel to make a part of a model into a stand-alone model
For the model described above, you may want to see how the vegetation part behaves, assuming fixed inputs from the animal and soil sections that affect it. You draw a submodel envelope around the vegetation, open up a separate window for it, then use the File: Save command to save it to a file. You can then start up Simile again, and load just the saved vegetation submodel (which is now a model in its own right). You can now explore how it behaves by itself. This can be very useful for testing and debugging purposes.
Using a submodel for modular modelling: swapping one module for another
For many years, the battle cry of those fed up with the implementation of models in computer programs was "modular modelling!". If we had a modular modelling system, it was argued, then models could be easily constructed from a number of pre-programmed modules, and the effectiveness of the community as a whole would be greatly increased by the sharing of these modules, avoiding huge duplications of effort.
The submodel concept in Simile supports modular modelling. You can open up a separate window for a submodel (say, a vegetation submodel); clear the contents of the submodel (by doing File: New), then load a different vegetation model into the submodel window. Influence links with the rest of the model can then be made one by one.
Furthermore, Simile supports plug-and-play modularity (which is what is normally meant by "modular modelling"). If two or more vegetation submodels have been designed to share a common set of influences (in and out) with the rest of the model, then the information about this interfacing can be stored in a file (an interface specification file). When you next load one of the submodels from a file, you simply refer to the interface specification file, and all the influence links are made in one quick operation.
Using a submodel for disaggregation;
or (conversely) specifying a fixed number of objects of a certain class
These two terms are lumped together because they are the same concept, seen from opposite perspectives. You can disaggregate an area into a number of patches; or you can think in terms of one patch, then have multiple patches to represent some larger area. The end result in both cases is exactly the same.
Once you have made a submodel you can specify (by going to its Properties dialogue box) that it is a "fixed-membership submodel", and specify a number of instances. In the "Control of number of instances" panel, select the "Using specified dimensions" radio button and enter the number you require. The submodel then represents each of that number of instances. Visually, it now appears different, because it now has multiple lines on the right- and bottom-edges: like a stack of cards. Internally, Simile now handles each instance separately: each can have its own parameter and initial values, while they all have the same compartments, flows etc.
This enables many forms of disaggregation to be captured. For example:
- disaggregating a population into age, size, or sex classes;
- disaggregating a vegetation component into the several species that make it up;
- disaggregating soil or forest canopy into a number of layers;
- disaggregating space into grid squares, polygons, or some other form of spatial unit.
Note that there are two further options in the pull-down menu: rectangular grid and hexagonal grid. These also correspond to fixed-membership submodels, but make special functions available within the submodel for capturing various properties of rectangular/hexagonal grids.
Using a submodel to specify a dynamically-varying population of objects
The modelling world divides into those whose models are based on differential/difference equations (with or without disaggregation); and those who subscribe to an approach based on collections of objects (variously called object-oriented, individual-based or agent-based modelling).
Simile enables a population approach to be combined with a differential-difference equation approach. For example, a modeller might represent the vegetation in terms of compartments and flows, while the herbivores might be represented as individual animals, which are created, grow and die. In order to do this, a submodel is specified as being a population submodel (Specify control of number of instances as "using population symbols" in its Properties dialogue box), and model elements can be added for specifying the initial number, and the rules for the creation of new individuals and the elimination of those already n the population. Visually, the submodel now appears with a shadow line for the top- and left-edges, and another for the bottom- and right-edges.
The remaining option for controlling instance numbers is "Using number of data records in file". This will set the number of instances according to the number of values provided for fixed parameters within that submodel, so the same model can be used for simulations involving datasets of different sizes.
Using a submodel to specify the conditional existence of some part of the model
When a model is implemented in a conventional programming language, large chunks of the program can be enclosed inside an if … end if block: i.e. whether it is actually evaluated depends on some condition. This programming device may be applied to several different purposes:
- You may want to have several alternative ways of modelling some part of the system (e.g. a growth function), only one of which is active in any one run of the model. A flag determines which one is active.
- You may want to model a set of species using a single submodel, but with only some species present in any one run of the model.
- You may want to model a number of spatial patches, some of which contain one land use type, and others of which contain another. You need to include a submodel for each one within the multiple-instance patch submodel - but switch one or the other on in a particular patch.
All these situations can be handled in Simile using a conditional submodel. This is simply a submodel, either simple or fixed-membership, but with a condition symbol added. Visually, we can tell that it's a conditional submodel both by the presence of the condition symbol, and by a set of dots going down diagonally to the right from the submodel envelope. The condition contains a Boolean expression: if this evaluates to "true", then the submodel (or an instance of it) exists; if not, then it doesn't.
A conditional submodel will, like any other, have influences coming out from the model elements it contains. However, the number of values passed along each influence could be anything from zero (if no instances of the model exist) to the number given in the fixed-membership specification (if they all do). It is thus a variable-size data structure: in other words, a list (with the name of the variable enclosed in curly braces {…} ). In Simile, the only thing that can be done with a list is to evaluate it: usually, to sum its values. If the list is empty, then the sum is zero. If the list contains a single element, then the sum is whatever this value is.
Using a submodel to specify an association between objects
Once our modelling language allows us to think in terms of multiple objects of a certain type, then it is frequently the case that we start to recognise relationships between objects. These relationships may be:
- between objects of the same type: one tree shades another; one grid square is next to another; one person is married to another; or
- between objects of one type and objects of another: one farmer owns a field; one field is close to a village.
Since Simile is a visual modelling language, and since such relationships are an important aspect of the design of a particular model, Simile provides visual elements to show diagramatically such relationships between objects. Unfortunately, the term "relationship" is normally used in ecological modelling to refer to a relationship between variables (as opposed to objects), so we use the term "association" instead. This is the same term used in UML (the Unified Modelling Language, the standard object-oriented design language used in the software-engineering community).
An association can itself have properties. We can, for example, have a variable representing the actual distance between a field and a village: this is a property of neither the field or the village, but of the association between them. In Simile, the submodel is the construct that is able to hold a number of quantities, therefore we use a submodel to represent an association: it is then called an association submodel.
However, such a submodel is simply a normal Simile submodel. It becomes an association submodel by virtue of being linked to the submodel (or submodels) representing the objects that have the association. The linking is done using role arrows: one role arrow is drawn for each type of object that participates in the association. Thus:
- for the owns association between farmer and field, we draw a single role arrow from the farmer submodel to the owns association submodel, and one from the field submodel to the owns association submodel;
- for the next to association between one grid square and another, we draw two role arrows from the grid square submodel to the next to association submodel: one role arrow represents the field under consideration, while the other represents its neighbour.
Using a submodel to specify a satellite relationship between one object and another
Let's say that you have a multiple-instance submodel containing information on the species and volume of a set of individual trees: each instance is one tree. You would like to find the total volume of all trees belong to species 1.
This is easy to do if you have model the trees using a fixed-membership submodel (i.e. assuming that you have a fixed number of trees). You simply take influence arrows from the species and volume variables inside the submodel to a variable outside (say total), and give total the equation:
total = sum(if [species]==1 then [volume] else 0)
[species] and [volume] are both arrays with the same number of elements, and Simile's array language matches them up.
This technique will also work if you use a population submodel to model the trees. But suppose you want to do several operations on only the trees of a particular species? Rather than apply the species condition each time, you can make a satellite submodel corresponding just to the individuals you are interested in. It would involve creating a new submodel for the species 1 trees, using a single role arrow from the tree submodel to this satellite submodel, and entering the condition "species==1". An instance of this submodel will be created for each tree of species 1, and not for the others. If you then take the "volume" value into the submodel, then you can extract the volumes just for species 1.
A satellite model with the appropriate condition can represent any subgroup of the instances in its base model, including cases where instances may become members or stop being members of the subgroup as the model runs.
Using a submodel to specify different time bases for different parts of a model
By default, Simile uses the same time step to update all the model state variables. However, if you are modelling a system containing trees and crops, then you might very well want to model the trees on an annual basis (time step of one year), and the growth of the crop on a weekly basis (time step of 1 week).
Simile enables you to specify a time step category for any submodel. For each new time step category that you request, Simile adds an extra Update every entry in the Run Control dialogue window, and that is where you specify the actual time step (e.g. 0.01) to be used for each category.
Using a submodel to allow iterative calculation of a function
Some calculations simply cannot be done within the system-dynamics paradigm, as they involve actions that are repeated until some indication of completion is achieved -- for instance, methods involving successive approximation.
These can be included in a Simile model by creating a submodel for the iterative calculation, and including an alarm symbol. This is a boolean valued component, and will cause all the variables in the submodel to evaluate repeatedly until it evaluates to 'true'. If the iteration involves values from the previous calculation step, these can be referenced using an influence arrow with the "Use values made in same time step" property.
In: Contents >> Graphical Modelling >> Object/agent based
Model diagram elements : Initialisation
 Initialisation
Initialisation
The Initialisation symbol is used to specify the initial number of individuals in a population submodel. It is sometimes called the Creation symbol, and belongs to the group of symbols known as channels. The symbol's icon represents the rising sun.
How to add an Initialisation symbol
The Initialisation symbol only has meaning in the context of a population submodel. Therefore, it makes sense to construct a population submodel first, then add the Initialisation to it. This is not strictly necessary: you can add the Initialisation first, then construct a submodel around it, then make the submodel into a population submodel, but it is better practice to construct the population submodel first.
See Adding node-type elements.
Rules
- You can have any number of Initialisation symbols in any one population submodel. The initial population count will be the sum of their values. You may use more than one when the initial population consists of subgroups with different properties. You can use the channel_is( ) function on the initialisation channels to indicate which group each individual belongs to, and set its properties accordingly.
- You do not need to have an Initialisation symbol in a population submodel. If you do not have one, then the initial number of instances for the population is zero. You would then have to have a migration symbol if you wanted your population ever to have any instances. (If you only had a reproduction symbol, then the population would never be able to get going, since reproduction only works for individuals already in the population.)
- The Initialisation symbol may receive influence arrows, but (usually) only from variables calculated at the start of the simulation run, whose values do not change. A typical application would be to initialise the number of instances in the population from some fixed environmental attribute, such as the soil type or the area of the system being modelled.
- It is possible to draw an influence arrow from the initialisation symbol to another element. The usual use of this is with the channel_is( ) function. Otherwise, the value of the initialisation symbol is always the number of individuals it caused to be created at the start of the run, even if the value of its expression changes as the model runs.
In: Contents >> Graphical Modelling >> Object/agent based
Model diagram elements : Migration
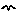 Immigration
Immigration
The Immigration symbol is used to specify the creation of new instances of a population submodel during the course of a simulation. In contrast to the Reproduction symbol, which specifies this in per instance terms (i.e. the creation of new instances per existing member of the population), the Immigration symbol determines the total number of new instances that are created. Note that the process adding new individuals need not be an actual immigration from another place -- it could be anything that causes new members of a population, unrelated to existing individuals, to appear throughout a run.
Immigration belongs to the group of symbols known as channels. The symbol's icon represents a bird on the wing.
How to add an Immigration symbol
The immigration symbol only has meaning in the context of a population submodel. Therefore, it makes sense to construct a population submodel first, then add the immigration symbol to it. This is not strictly necessary: you can add the immigration symbol first, then construct a submodel around it, then make the submodel into a population submodel, but it is better practice to construct the population submodel first.
See Adding node-type elements.
Rules
- The immigration symbol can receive influence arrows from anywhere in the model, including from within the same submodel. This information is then be used to calculate the current value for the rate of creation of new instances of the population. If the influence arrow comes from within the same population, then this input will be presented (in the Equation dialogue window) as a list, not as a scalar. See below for the reasons for this, and what you should do about it.
- You can include as many immigration symbols as you like. In real-world terms, each one corresponds to a separate process leading to the new instances being created: for example, some new trees can appear in a forest from seeds blowing in from outside the forest, while others can appear from a forester planting seedlings.
- It is possible to draw an influence arrow from the immigration symbol to another element. The usual use of this is with the channel_is( ) function. The value of the immigration symbol is the value of its equation.
Interpretation
The immigration symbol it is used to determine the creation of new instances of a population submodel. This must be in terms of whole numbers: you cannot have a part of a new individual. And yet, the value for the immigration term can be a floating-point number, e.g. 1.3. So how does Simile use this value to calculate the creation of new instances?
The value of the immigration symbol's equation is the number of new instances created over the course of one time unit. Typically the time step is not the same as a time unit, so each time step the value of an internal variable is incremented by the immigration symbol's value divided by the number of time steps in a time unit. If this value is one or greater, the integer part of the number is subtracted from it and that number of new individuals are added to the population. The fraction part remains to be incremented on the next time step.
In order that a model with many immigration processes behaves realistically rather than adding all new individuals synchronously, the internal variable for each one is initialized to a random fraction between 0 and 1. Thus there is a possibility that a new individual will arrive through immigration in any time step, even if the value of the channel is small.
Immigration events
An immigration symbol can be either continuous or discrete event valued. If any influences from events or squirts terminate on the immigration symbol, it is discrete event valued. In this case it will be evaluated in the same way as an event or squirt. When the event occurs, the value will be added to the latency (fraction remaining after previous additions) and new individuals added to the popualtion immediately if the result is 1 or greater.
Avoiding random behaviour
You might well feel uncomfortable with the non-deterministic nature of the process. To avoid any random variation between runs, you can make sure that the value of the equation for immigration divided by the number of time steps in a time unit is always a whole number, which will result in exactly that number of individuals being added each time step. The length of the time step is selected when running the model, and can be found with the dt() function.
If using discrete event valued immigration channels, all you need to do is make sure the event magnitude is integer valued, as the time step size does not affect the result of an addition event.
In: Contents >> Graphical Modelling >> Object/agent based
Model diagram elements : Reproduction
 Reproduction
Reproduction
The reproduction symbol is used to specify the rate of creation of new instances of a population submodel by each existing instance. It thus differs from the migration symbol, which specifies the total rate of creation of new instances. It belongs to the group of symbols known as channels. The symbol's icon represents an egg.
How to add a Reproduction symbol
The reproduction symbol only has meaning in the context of a population submodel. Therefore, it makes sense to construct a population submodel first, then add the reproduction symbol to it. This is not strictly necessary: you can add the reproduction symbol first, then construct a submodel around it, then make the submodel into a population submodel, but it is better practice to construct the population submodel first.
See Adding node-type elements.
Rules
- The reproduction symbol can receive influence arrows from anywhere in the model, including from within the same submodel. This information can then be used to calculate the current value for the rate of creation of new instances of the population. As with all other relationships within a population submodel (except for the migration symbol), influences coming from within the same submodel relate to the properties of the same instance. So, for example, an influence from a variable "bodyweight" to the reproduction symbol indicates that it is each individual's body weight that influences its own rate of reproduction.
- You can include as many reproduction symbols as you like. Biologically it is unusual to have more than one method for reproduction (though some organisms reproduce asexually and sexually at different stages of their life cycle), but it is perfectly legal as far as Simile is concerned.
- It is possible to draw an influence arrow from the reproduction symbol to another element. The usual use of this is with the channel_is( ) function. The value of the reproduction symbol is the value of its equation.
Interpretation
The reproduction symbol captures the concept that, in many biological situations, the production of new individuals by those already in the population - reproduction - is an important mechanism for increasing population size. Moreover, the ability of an individual to reproduce will depend on its own characteristics: its age or weight, for example.
As with the migration symbol, Simile needs to resolve the fact that the value for reproduction is a floating point number, while new individuals can only be created one-by-one. The method it uses to do this is similar to that used for migration, and essentially involves the use of the reproduction term to contribute fractions of an individual to an accumulator: when the accumulator exceeds a whole number, then that number of new instances for the submodel are created, and the accumulator is reduced by the number of instances created.
There is, however, an important issue that the designers of Simile had to address. Should there be one accumulator for the whole population, or one for each of the current set of instances? In the former case, if you had five instances, each with a reproduction value of 0.1, then one new individual would be created every 2 time units. In the latter case, for the same settings, you would get no new instances for ten time units, then five would be created at the same time. The first approach seems more attractive, but suffers from a fatal flaw: it assumes that the parentage of newly-created individuals is irrelevant. This would severely restrict the modelling you could do: in particular, it would rule out modelling evolution, since that requires some concept of (biological) inheritance, which in turn means that each individual needs to know who its parent(s) are. Also, the second approach gives the same behaviour as the first if the value for reproduction is treated stochastically (e.g. as a probability), rather than as a precise deterministic contribution until you have enough credit to make one individual. Therefore, in Simile, each individual accumulates its own credit, starting with a random fraction, until it has sufficient to make one new individual.
Like migration channels, reproduction channels can be discrete event valued. If the event that triggers a reproduction event is outside the population submodel, then when it occurs, all individuals in the population will reproduce, subject in each case to the equation of the reproduction channel having a positive value. Alternatively the triggering event can be inside the population submodel, in which case only the individuals in which the event occurs will reproduce.
As in the case of the migration symbols, the accumulators are initialized to random fractions between 0 and 1. This ensures that if the reproduction rates are the same in a lot of individuals, the new ones do not all appear in the same time step but in a random pattern with no pre-determined peaks or troughs. If this non-deterministic behaviour is not required, the technique described for deterministic migration can be used to eliminate it.
In: Contents >> Graphical Modelling >> Object/agent based
Model diagram elements : Extermination
 Extermination
Extermination
The extermination symbol is used to specify the conditions under which one instance of a population submodel ceases to exist. It is sometimes called the loss or mortality symbol. It belongs to the group of symbols known as channels. The symbol's icon represents an axe.
How to add a Extermination symbol
The extermination symbol only has meaning in the context of a population submodel. Therefore, it makes sense to construct a population submodel first, then add the mortality symbol to it. This is not strictly necessary: you can add the mortality symbol first, then construct a submodel around it, then make the submodel into a population submodel, but it is better practice to construct the population submodel first.
See Adding node-type elements.
Rules
- The mortality symbol can receive influences from anywhere in the model, both inside and outside the population submodel of which it is a part. This means that the chances of an individual instance being destroyed can depend on both factors that are external to the population, and on the characteristics of that particular individual.
- There can be multiple mortality symbols in the same population submodel.
- It is possible to draw an influence arrow from the mortality symbol to another element. The usual use of this is with the dies_of( ) function. The value of the mortality symbol is the value of its equation.
Interpretation
A mortality channel represents a 'risk factor' for the individuals in its population. Its value should be a fraction between 0 and 1, and this represents the probability of the individual for whom it has that value being removed over one time unit. In this sense it works like radioactive decay; the individuals do not 'lose health' before they die, but rather any surviving individual's chance of dying is determined solely by its current mortality, no matter what it has been in the past. Note that this is different from the behaviour of the migration and reproduction channels, where the rate is summed over multiple time steps. If you require your model to capture a situation in which individuals do die as a result of losing health, the process of health loss must be represented explicitly in the model, with the mortality channel only becoming nonzero when they actually go.
The rate of removal is spread over every time step; if there are 10 time steps in a time unit, and an individual's mortality is 0.3, then there is a roughly 0.03 (exactly 1- (1-0.3)0.1) chance of removal in each time step. Multiple mortality channels act independently; if there are two, and for a given individual they each have a value of 0.5 over a time unit, then the probability of that individual being removed in that time unit is 0.75. A value of 1 in any time step makes it certain that the individual will be removed in that time step.
Individuals are removed at the start of the time step following the one in which their number came up. This means other values from their submodel instances can be used in that time step. A function is available in the equation language, dies_of(), which returns true if the argument is from a mortality symbol that results in the individual's removal in that time step (cf. channel_is( ))
A removal channel can also be discrete-event valued, if it has an influence from an event or squirt. In this case, when the triggering event happens, individuals may be removed immediately. The magnitude of the removal event is the probability, as a fraction of 1, that the individual will be removed at that point. If the value is 1 or greater, removal is certain. In order to avoid any random behaviour in a model containing removal channels, they should only ever have values of 0 or 1. Removal symbols, whether discrete or continuous valued, can have boolean units ("true" or "false") which have the same effect as 1 and 0.
In: Contents >> Graphical Modelling >> Object/agent based
Model diagram elements : Role arrow
 Role arrow
Role arrow
How to add a Role arrow
See Adding arrow-type elements.
Interpretation
Role arrows join submodels that participate in some form of association, or where one is a satellite of the other. The following sections detail the mathematical methods invoked by the role arrow. In each case, a multi-dimensional matrix is created containing instances of the submodel at the head of the role arrow. The dimensions of the matrix depend on the number of role arrows used, and the different uses are therefore described in separate sections.
Rules
- A role arrow can only be drawn between two submodels, one representing the object that plays a role in an association, and the other representing the association itself.
- Role arrows cannot be added in such a way that they form a loop.
In: Contents >> Graphical Modelling >> Object/agent based
Role arrow : Single role arrow
 Single role arrow
Single role arrow
Using a single role arrow to connect two submodels is almost exactly equivalent to nesting one submodel inside the other. In effect, the submodel that the role arrow points to, is nested inside the submodel that the role arrow points from. This alternative diagram form is useful because of the extra flexibility it allows in laying out the model diagram. It is also helpful to understand this simple use of role arrows before using them in more complex ways.
The following model diagram illustrates the relevant features of the use of a single role arrow to connect two submodels. In this case, one submodel is called "Base" (or "Master"), and the role arrow points from it, to the other submodel, called "Satellite". "Base" is a multiple-instance submodel, with fixed dimensions. In the following example, there are ten instances of "Base". Inside "Base" there is a variable called "index". The equation for "index" is "index(1)". The variable "index" therefore has a unique value within each instance of "Base".
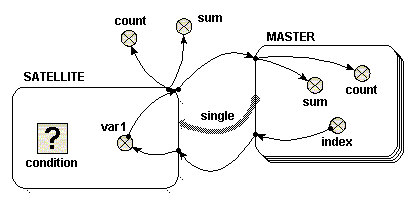
When adding the equations for this model, you will notice that the role arrow is having an effect on the parameter names corresponding to influences that come from inside a submodel at its far end. First, have a look at "var1" in the "Satellite" model. Now, if the role arrow were not present, the only available parameter name for this would be "[index]", representing an array of the values of "index" in the 10 instances of "Master". However, with the role arrow present, you can use the parameter name "single_index", made by combining the names of the role arrow and source component. This is a scalar quantity, and has the value of "index" in the particular instance of "Master" associated with each instance of "Sattelite". It is as if "Satellite" were a simple submodel inside "Master", with one instance for each instance of its parent. (Note, if using Simile v5.7 or later, the parameter name "[every_index]" is also available, which stands for the array of 10 values that you would get if the role arrow were not present. In versions 6 and on, the availability of the different interpretations of an influence can be enabled or disabled in the influence properties dialogue -- see Influences and Roles).
Something similar happens for influences going in the other direction from the role arrow. Now, look at "sum" in the "Master" model. The parameter name "{var1_single}" is available. The curly brackets indicate that this stands for a list of values -- but because the role arrow is used, the list will contain only the values from instances of "Satellite" associated with each particular instance of "Master". In this case, that means at most one instance, and hence one value, for each instance of the base model. (Again, if using Simile v5.7 or later, the parameter name "{every_var1}" is also available, which stands for the list containing values from all instances of the associated model).
Now let's look at what happens on execution. To start with, consider a case in which the  condition symbol in "Satellite" is omitted (or equivalently, where it has an equation whose value is always "true", such as 1>0). In this case, ten instances of "Satellite" are created, the same as the number of instances of "Base". Inside "Satellite" is a variable called "var1". There is an influence arrow from the variable "index" in "Base" to "var1", and its equation is simply "single_index". The value of "var1" in each instance of Satellite is therefore equal to the "index" of the equivalent instance of "Base".
condition symbol in "Satellite" is omitted (or equivalently, where it has an equation whose value is always "true", such as 1>0). In this case, ten instances of "Satellite" are created, the same as the number of instances of "Base". Inside "Satellite" is a variable called "var1". There is an influence arrow from the variable "index" in "Base" to "var1", and its equation is simply "single_index". The value of "var1" in each instance of Satellite is therefore equal to the "index" of the equivalent instance of "Base".
To illustrate how "var1" is treated, there are four influence arrows taken from it. Two influence arrows point to variables "count" and "sum" within "Base" and two point to variables "count" and "sum" outside "Base". There is an important difference in the values received in these two circumstances, which is easy to understand if you consider "Satellite" is treated as if it were nested inside "Base".
- Inside "Base", the equation "count({var1_single})" returns 1, and "sum({var1_single})" returns a value equal to "index" of the same instance.
- Outside "Base", the equation "count({var1})" returns 10, and "sum({var1})" returns a value equal to sum of the index of all the instances, i.e. 55, in this case (calculated from 1+2+3+…+9+10)
Beware one point: both inside and outside "Base", the value returned from "Satellite" is received as a list, even if there is no condition symbol in the satellite. An integrating function such as sum() or count() must be used immediately on a list. Inside "Base", the list consists of a single number, so sum({var1_single}) returns the value of the number. The reason for using a list is that the list may in fact be empty, rather than containing a single value, for reasons described below. Note that curly braces are used to denote the list.
Now consider a simple equation for the condition symbol. In the example given, the condition symbol has no influence arrows pointing to it, though it can have. Suppose one wishes "Satellite" to exist for only the odd-numbered instances of "Base". In this case, the equation "fmod(index(1),2)==1" or "index(1)%2==1" would be used. Note that the index() function used within "Satellite" refers to the index of the equivalent instance of "Base".
Using the condition symbol in this or other ways permits the number of instances of "Satellite" to be less than the number of instances of "Base". There can never be more instances of "Satellite" however than instances of "Base", unless the satellite submodel has dimensions of its own.
In the example chosen above, in which only odd-numbered instances of "Satellite" are created, the four influence arrows behave like this.
- Inside "Base", the equation "count({var1_single})" returns either zero or one. It returns one, only if this is an odd-numbered instance, i.e. for instances 1, 3, 5, 7 and 9. Otherwise it returns zero. In these cases, i.e. instances, 2, 4, 6, 8 and 10, the list is an empty list. Similarly, the equation "sum({var_single})" returns either zero or a value equal to "index" of the same instance. It returns zero for each empty list, i.e. instances 2, 4 ,6, 8 and 10.
- Outside "Base", the equation "count({var1})" returns five. The equation "sum({var1})" returns 25 (calculated from 1+3+5+7+9).
When using the condition symbol in "Satellite", the use of the role arrow is more convenient than the equivalent nested arrangement. If "Satellite" were nested inside "Base" it would not be possible directly to receive the list in a variable outside "Base" -- you would instead get an array of lists.
Many satellite instances per base instance
In the above example, the satellite submodel does not have any dimensions of its own. It only has multiple instances because the base model does, and each base model instance can have at most one associated satellite submodel instance. But you can set dimensions for the satellite model, in which case each base model instance can be associated with up to this number of satellite model instances.
If you do this, then for equations inside the satellite submodel, index(1) means the index of that instance within the group associated with its base model instance, while index(2) means the index of the base model instance (as long as the satellite submodel has only one dimension).In other words, the value that is index(1) in a base model index is available as index(2) in its satellite model instances.
As an example, you could create a model where base instance 1 has 1 satellite instance, base instance 2 has 2, and so forth. The satellite would have dimensions 10 and the condition equation would be "index(1) <= index(2)". In the satellite, "var1" still has the index value of the corresponding base model. There would then be 1+2+...+10 == 55 satellite instances, and the value of "sum" outside the submodels would be 1*1 + 2*2 + ... + 10*10 = 385. Another example: set the condition equation to "index(1) >= index(2)". Now, base instance 1 will have 10 satellite instances, instance 2 has 9 and so forth. There are still 55 satellite instances, but "sum" is now 1*10 + 2*9 + ... + 10*1 = 220.
In : Contents >> Model diagram elements >> Role arrows
Role arrow : Two role arrows from different submodels
 Two role arrows from different submodels
Two role arrows from different submodels
If a single role arrow between two models can be compared to nesting one submodel inside the other, using two role arrows to link submodels both to a third can be compared to creating an area where the two submodels overlap and are interleaved with each other. From the point-of-view of "Object A", "Object B" is nested within "Object A". From the point-of-view of "Object B", "Object A" is nested within "Object B".
The following model diagram illustrates some of the features of this arrangement. Two multiple-instance submodels are created, "Object A" with two instances, and "Object B" with three. Both these objects are linked with role arrows to the third submodel "Association". One instance of "Association" is automatically created for each possible pair of instances of "Object A" and "Object B".
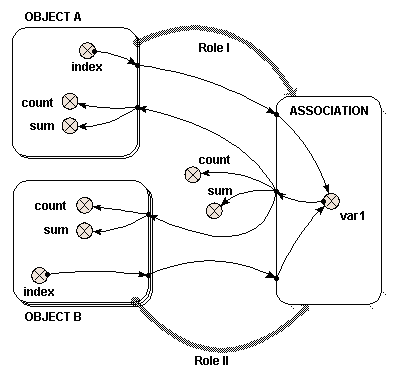
In this case, there are six instances of "Association", resulting from the two "Object A" and the three "Object B". Inside "Association" is a variable "var1". The two variables that influence "var1" have the full path names "../Object A/index" and "../Object B/index", and each has been set to the index of its own submodel with the equation "index(1)". The instance of "Object A" and the instance of "Object B" from which each "index" is taken is determined by the instance of "Association". Each instance of "Association" receives one of the six possible pairs of the "index" variables.
Local names for the two different full path names are created to avoid duplication, and to avoid using illegal characters such as spaces in the equation. In this case we have changed the local names to be "indexA" and "indexB" to avoid confusion, as described in the help page. In this simple example, the equation for "var1" is "indexA*indexB".
If this were represented by a table, it would look like this:
|
Object A - instance 1 indexA" = 1 |
Object A - instance 2 "indexA" = 2 |
|
|
Object B - instance 1 "indexB" = 1 |
Association - instance 1 "Var1" = 1 |
Association - instance 4 "Var1" = 2 |
|
Object B - instance 2 "indexB" = 2 |
Association - instance 2 "Var1" = 2 |
Association - instance 5 "Var1" = 4 |
|
Object B - instance 3 "indexB" = 3 |
Association - instance 3 "Var1" = 3 |
Association - instance 6 "Var1" = 6 |
The order of the instances in "Association" is determined by the order in which the role arrows are added. It is not usually important, but selecting "allow base instance lookup" in a role arrow's properties will ensure that "index(1)" in an equation in the association submodel refers to the indices of that arrow's base submodel. To understand how "var1" is represented, six influence arrows are taken from "var1" to different parts of the model.
- Inside "Object A"
|
{var1} |
count({var1}) |
sum({var1}) |
|
|
Instance 1 |
{1 2 3} |
3 | 6 |
|
Instance 2 |
{2 4 6} |
3 | 12 |
- Inside "Object B"
|
{var1} |
count({var1}) |
sum({var1}) |
|
|
Instance 1 |
{1 2} |
2 | 3 |
|
Instance 2 |
{2 4} |
2 | 6 |
|
Instance 3 |
{3 6} |
2 | 9 |
To understand where both these sets of results for "{var1}" come from, look down (for "Object A") or across (for "Object B") the relevant lines of the full six instance "Association" table given above. The count() and sum() functions operate on the given {var1} to produce the results shown.
- Outside both "Object A" and "Object B"
|
{var1} |
count({var1}) |
sum({var1}) |
|
|
{1 2 3 2 4 6} |
6 | 18 |
As with the use of a single role arrow, the  condition symbol will permit the number of instances of "Association" to be less than the product of the number of instances of "Object A" and "Object B". The Boolean expression used in the condition symbol can involve influences from other model elements and can use the index(x) function to return the instance of both "Object A" and "Object B", using x=1 and x=2 respectively.
condition symbol will permit the number of instances of "Association" to be less than the product of the number of instances of "Object A" and "Object B". The Boolean expression used in the condition symbol can involve influences from other model elements and can use the index(x) function to return the instance of both "Object A" and "Object B", using x=1 and x=2 respectively.
In : Contents >> Model diagram elements >> Role arrows
Role arrow : Two role arrows from the same submodel
 Two role arrows from the same submodel
Two role arrows from the same submodel
The most common use of the role arrow is (unfortunately) the most difficult to visualise. In this case, two different instances of the same object play two different roles in an association. One might think of this as being like each instance having all the other instances nested within it.
In the case of the single role arrow, or the case of two role arrows from two objects, the role itself was not an important element. The role arrow represented graphically the nesting arrangement. In this case however, the names of the two different role arrows are the only means of distinguishing the instances of the single object within the association submodel.
The following model diagram illustrates a simple example of the use of the association submodel in this way. There is an "Object" submodel, which has three instances. Two role arrows, "Role I" and "Role II", link "Object" to the "Association" submodel.
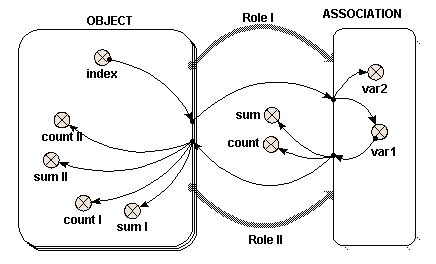
In this case, nine instances of "Association" are created, one for each possible pair of instances of "Object". Inside "Association" are two variables "var1" and "var2". Each of these receives a single influence arrow from the "index" variable in "Object", BUT, look at the list of parameters in the equation dialogue box, and two are given. These two parameters refer to the "index" variable in each of the members of the pair of instances of "Object" that generate this instance of "Association".
A unique local name for each parameter is automatically generated, but to avoid confusion, right click on each local name to rename it indexI and indexII, for "Value(s) of ../Object/index (from Object in Role I)" and "Value(s) of ../Object/index (from Object in Role II)" respectively. In this example, "var1" is given the expression "indexI" and "var2" is given the expression "indexII".
If this were represented as a table, it would look like this:
|
Object in Role I "indexI" = 1 |
Object in Role I "indexI" = 2 |
Object in Role I "indexI" = 3 |
|
|
Object in Role II "indexII" = 1 |
var1 = 1 var2 = 1 |
var1 = 2 var2 = 1 |
var1 = 3 var2 = 1 |
|
Object in Role II "indexII" = 2 |
var1 = 1 var2 = 2 |
var1 = 2 var2 = 2 |
var1 = 3 var2 = 2 |
|
Object in Role II "indexII" = 3 |
var1 = 1 var2 = 3 |
var1 = 2 var2 = 3 |
var1 = 3 var2 = 3 |
So far, the results are rather similar to those where two objects are involved. This is also true of what follows, though it is less obvious. To understand how "var1" is represented, six influence arrows are drawn from it to different parts of the diagram. (Symmetrical results are generated using "var2", though these are not given here.)
| OBJECT | Values of var1 for role I | sum | count | values of var1 for role II | sum | count |
|
Instance 1 |
{1 1 1} |
3 | 3 |
{1 2 3} |
6 | 3 |
|
Instance 2 |
{2 2 2} |
6 | 3 |
{1 2 3} |
6 | 3 |
|
Instance 3 |
{3 3 3} |
9 | 3 |
{1 2 3} |
6 | 3 |
The  condition symbol can be used inside "Association" to permit fewer instances than the square of the number of instances of "Object" to be generated, and thus pass values between base instances selectively.
condition symbol can be used inside "Association" to permit fewer instances than the square of the number of instances of "Object" to be generated, and thus pass values between base instances selectively.
Inside the association submodel, the index(x) function returns the index of each of the members of the pair of instances that generate this instance of "Association" with x = 1 for "Dimension 1 of Object (3) in Role II for Association" and x = 2 for "Dimension 1 of Object (3) in Role I for Association". To identify which index refers to the use of which role arrow, see the indices panel on the Parameters tab of the equation dialogue box.
Note that the "(3)" is the size of the given dimension. Influences from other elements can also be used in the Boolean expression for the condition symbol.
In : Contents >> Model diagram elements >> Role arrows
Model diagram elements : Condition
 Condition
Condition
A condition model element is used to specify whether a submodel, or a potential instance of a multiple-instance submodel, actually exists.
How to add a Condition symbol
The condition symbol only has meaning inside a submodel. Therefore, you should make the submodel first, then add the condition symbol to it. This is not strictly necessary: you can add the condition symbol first, then construct a submodel around it, but it is better practice to construct the submodel first.
See Adding node-type elements.
Rules
- A condition element only has use within a submodel (since it specifies which potential instances exist). It should not appear in a population or per-record submodel because these have their own means of creating and destroying instances.
- The expression in the equation dialogue box for a condition element is a Boolean expression: that is, it returns the value "true" or "false". This normally takes the form of some sort of comparison, using the conditional operators such as >, <, >= etc, combined with logical operators such as "and" and "or". However, conditions of the form "index(1) is <expr>" or "any(index(1) is <list_expr>)" are also allowed; see one-sided relation enumeration.
- A condition may have influences to it from anywhere in the model. It cannot have influences from it, since either its value is "true" or its submodel instance does not exist.
- If a condition is inside a simple submodel, then that submodel either exists or not, depending on the result of evaluating the condition's expression.
- If a condition is inside a fixed-membership submodel, then each instance of the submodel may exist or not, depending on the condition's expression (which would make use of the built-in function index to refer to particular instances).
- If the condition model element is inside an association submodel, then the relation exists between a particular pair of object instances only if the condition's expression evaluates to "true" for that pair. The condition's equation can use values from base instances in particular roles in order to set the association to exist only if the base instances' values match in a certain way.
In: Contents >> Graphical Modelling >> Object/agent based
Model diagram elements : Iteration
 Iteration
Iteration
An iteration model element makes its parent submodel an iterative submodel, whose contents should be evaluated repeatedly until a finishing condition is met.
How to add an Iteration symbol
See Adding node-type elements.
Rules
The iteration symbol contains the condition that marks the successful convergence of the iteration. On each time step of the model, after the compartment values have been adjusted, the values of all variables are calculated as normal. Then if the alarm symbol's equation evaluates to "false", the variables in its submodel are calculated again, and the test repeated, until it evaluates to "true" at which point the loop exits. See iterative submodel for a full description with examples, but a simple case of evaluation by successive approximation could be implemented as follows.
An influence arrow coming from the alarm symbol can be used as an argument to the function iterations( ). This function returns the number of iterations made so far. This function can be used to set the initial value (also called the guess) for the loop, i.e. when the number of iterations so far is equal to zero. This can also be set if the value of the alarm is "true" since this is how it is left at the end of the previous time step. If the number of iterations so far is one or more, or if the value of the alarm is "false", then the result of the last calculation should be used. Since the last calculation depends on the result calculated from the guess, a circular loop of influences is present. Normally, Simile would reject this loop at build time, but setting a property of the influence arrow: "Use values made in same time step" to true, allows the loop to be processed. Influence arrows with this property set are drawn with a dashed line. To set this property for an influence arrow, double-click on it to invoke the property dialogue box.
Note that if the value of the alarm symbol is used directly to decide if the initial guess should be used, then its influence should also be dashed, as the value of the alarm symbol is set by a test on the result. This is not necessary if using the "iterations()" function, which does not check for circularity involving its argument.
- The expression in the equation dialogue box for an iteration element is a Boolean expression: that is, it returns the value "true" or "false". This normally takes the form of some sort of comparison, using the conditional operators such as >, <, >= etc, combined with logical operators such as "and" and "or".
In: Contents >> Graphical Modelling >> Object/agent based

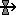
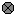
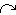
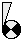 Parameter (a coefficient in an equation): e.g. the reproductive rate per individual animal. Could also be a site constant: e.g. elevation above sea level. Its value will remain constant throughout a simulation run.
Parameter (a coefficient in an equation): e.g. the reproductive rate per individual animal. Could also be a site constant: e.g. elevation above sea level. Its value will remain constant throughout a simulation run. Input lever: a
Input lever: a  Limit event : This represents an event that occurs when a model value reaches some pre-set limit. It requires an equation and a minimum and/or maximum value to be entered. The event occurs when the value of the equation reaches the minimum or maximum, and the event should cause the value to go no further in that direction. The event is boolean (i.e., has no magnitude) if only one limit is present. If both are present its magnitude is -1 at the lower limit and 1 at the upper limit. Hence its equation does not affect its magnitude, only its time of occurrence.
Limit event : This represents an event that occurs when a model value reaches some pre-set limit. It requires an equation and a minimum and/or maximum value to be entered. The event occurs when the value of the equation reaches the minimum or maximum, and the event should cause the value to go no further in that direction. The event is boolean (i.e., has no magnitude) if only one limit is present. If both are present its magnitude is -1 at the lower limit and 1 at the upper limit. Hence its equation does not affect its magnitude, only its time of occurrence. Time series: This gets its values from outside the model like a
Time series: This gets its values from outside the model like a  'zap' button.
'zap' button.