abs function

abs(X)

Returns the absolute value of X - i.e. ignores its sign

Input: numeric scalar or numeric array

Result: numeric scalar or array

Examples:

abs(3) --> 3

abs(-3) --> 3

abs([2,-3,4,-5]) --> [2,3,4,5]

In: Contents >> Working with equations >> Functions >> Built-in functions

pow function

pow(X,Y)

Returns X raised to the power Y

Input: numeric, numeric

Result: numeric

Comment:

This is equivalent to the use of the ^ operator: i.e.

pow(5,2)

is the same as

5^2

The latter should be used of preference, as it is the more familiar notation.

In: Contents >> Working with equations >> Functions >> Built-in functions

min function

min(X,Y)

Returns lesser of X and Y; i.e. it returns X if X<=Y, otherwise it returns Y.

Inputs: numeric, numeric

Result: numeric

Comments:

The min function is a useful way of ensuring that some value does not go above some threshold. For example, if b increase as a increases, but does not exceed 20, then the equation for b could be:

b = min(20, 0.2*a)

This avoids the use of a cumbersome if…then… else… construction

In: Contents >> Working with equations >> Functions >> Built-in functions

max function

max(X,Y)

Returns greater of X and Y; i.e. it returns X if X>=Y, otherwise it returns Y.

Inputs: numeric, numeric

Result: numeric

Comments:

The max function is a useful way of ensuring that some value does not go below some threshold. For example, if b declines as a increases, but does not go below zero, then the equation for b could be:

b = max(0,10-0.2*a)

This avoids the use of a cumbersome if...then...else... construction.

In: Contents >> Working with equations >> Functions >> Built-in functions

sqrt function

sqrt(X)

Returns the square root of X

Input: numeric

Result: numeric

In: Contents >> Working with equations >> Functions >> Built-in functions

round function

round(X)

Rounds X up or down to the nearest whole number

Input: numeric, or array of numeric values

Result: numeric, or array of numeric value

Examples:

round(1.9) --> 2

round(1.1) --> 1

round([1,2.1,3.9]) --> [1,2,4]

In: Contents >> Working with equations >> Functions >> Built-in functions

log10 function

log10(X)

Returns base-10 logarithm of X

Input: numeric

Result: numeric

In: Contents >> Working with equations >> Functions >> Built-in functions

log function

log(X)

Returns natural logarithm of X

Input: numeric; or an array of numeric values

Result: numeric; or an array of numeric values

In: Contents >> Working with equations >> Functions >> Built-in functions

ceil function

ceil(X)

Rounds up X to the next whole number (stands for 'ceiling')

Input: numeric, or array of numeric values

Result: numeric, or array of numeric value

Examples:

ceil(1.9) --> 2

ceil(1.1) --> 2

ceil([1,2.1,3.9]) --> [1,3,4]

In: Contents >> Working with equations >> Functions >> Built-in functions

exp function

exp(X)

Returns e (the base of natural logarithms) to the power X

Input: numeric, or an array of numeric values

Result: numeric, or an array of numeric values

Example:

The exponential growth of a population is given by the formula

N_t = N₀e^r.t

where:

N_t is the population size at time t,

N₀ is the initial population size,

e is the base of natural logarithms,

r is the intrinsic growth rate, and

t is current time
 

We can represent this in Simile using a single variable (called N), with its equation being

N = 10*exp(0.1*time(1))

assuming that the initial population size = 10 and the value of r is 0.1.
 

In: Contents >> Working with equations >> Functions >> Built-in functions

floor function

floor(X)

Rounds X down to a whole number.

Input: numeric, or an array of numeric values

Result: numeric, or an array of numeric values

Examples:

floor(3.1) --> 3

floor(3.99) --> 3

floor([1.1,2.4,3.7,4.9]) --> [1,2,3,4]

In: Contents >> Working with equations >> Functions >> Built-in functions

int function

int(X)

Returns integer part of X

Input: numeric

Result: numeric

In: Contents >> Working with equations >> Functions >> Built-in functions

hypot function

hypot(X,Y)

Returns length of hypotenuse of right-angle triangle with base X and height Y

Inputs: numeric, numeric

Result: numeric

Examples:

hypot(3,4) --> 5 (a 3:4:5 triangle)

hypot(x1-x2,y1-y2) --> the distance between two points with co-ordinates (x1,y1) and (x2,y2) respectively.

hypot(x-[xs],y-[ys]) --> [distances] I.e. an array containing the distance from one point with co-ordinates (x,y) to a set of points, with co-ordinates held in the arrays [xs] and [ys]. See comments.

Spatial modelling frequently requires that one object knows the distance to another. This requires that each has x,y co-ordinates. It is then simple to use the hypot function to work out the straight-line distance between them, as shown in the second example above.

The same principle applies when you use a multiple-instance submodel to represent a set of spatially-located objects. In this case, each object may want to know how far it is to all the other objects - for example, in working out the competition between trees in an individual-based tree model. The following model diagram fragment shows a typical model configuration for doing this:

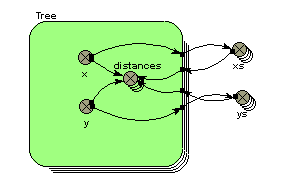
Each tree has x,y co-ordinates. These are exported to two array variables, xs and ys, whose equations are simply:

xs = [x]

and

ys = [ys]

These arrays are then brought back into the submodel, and used to generate an array containing the distance for each tree to all the other trees, using the equation given in the third example above.

In: Contents >> Working with equations >> Functions >> Built-in functions

fmod(X,Y)

Returns remainder after dividing X by Y

Inputs: numeric, numeric

Result: numeric

Examples:

fmod(7,3) --> 0.333 (7/2 = 2.333, i.e. the remainder is 0.333)

fmod(time(1),1) --> a result that climbs from 0 to 1 repeatedly (i.e. a sawtooth pattern) as the simulation proceeds. See comments below.

fmod((index(1)-1),5)+1 --> 1,2,3,4,5,1,2,3,4,5,1,2,3... for successive values of index(1). See comments below.

This apparently obscure function in fact has (at least) two very valuable uses.

First, it can be used to generate regular cycles, in particular annual or daily cycles. Consider the case or a model with the time unit being one year, and a time step of less than a year. You want various exogenous variables (such as temperature or rainfall) to vary in a prescribed fashion during the course of each year, with the annual pattern repeating itself from one year to the next. The following diagram is typical of the model fragment you could use for representing this:

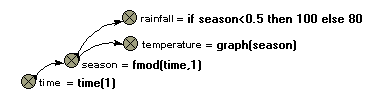
The variable time is simply set equal to current simulation time, using the function time(1). The variable season is set to rise from 0 to 1 every year. If your model used a time unit of one week, then the equation would be changed to

season = fmod(time,52)

and the value for season would then correspond to week number. The equations for rainfall and temperature are for illustration purposes only: you would need to replace them by something appropriate.

Second, the fmod function can be used to generate a regular spatial arrangement (rows and columns) for a 2D grid. Let's say that you are modelling an area of 10x10 grid squares. In Simile, you would set up a submodel, called perhaps Patch, with 25 instances. In order to give each patch location on a grid, each one needs to have a row and column attributes, with each patch having a unique combination of the numbers 1..5 for row and column. The only thing we know about each patch is that it has an index number (given by the built-in function index(1)), a value ranging between 1 and 25. The trick is to get row number to be, in sequence,

1,1,1,1,1,2,2,2,2,2,3,3,3...

and column number to be, in sequence,

1,2,3,4,5,1,2,3,4,5,1,2,3...

thus giving each of the 25 instances a unique row-and-column pair.

This is readily done using the following two equations:

row = floor((index(1)-1)/5)+1

column = fmod((index(1)-1),5)+1

See the floor function to understand why the row numbers should be in the first sequence above. For column, we divide the index number for each instance by 5, taking the remainder: the '-1' and +1' are there to ensure that we get the results in the blocks of five that we require. See a grid-based spatial model example to see this in action.

In: Contents >> Working with equations >> Functions >> Built-in functions